Geometria Płaska FischerPrise: Pole prostokąta jest równe 9 cm(kwadratowych) , a średnica okręgu opisanego na tym prostokącie ma długość 6 cm. Oblicz miarę kąta ostrego między przekątnymi prostokąta.

ICSP: a,b − boki, α − kąt między przekątnymi

	1		1		1
P =		*3*3*sinα =		*a*		b
	2		2		2

9		1
	sinα =		ab
2		4

	2		1		1		9		1
sinα =		*		ab =		ab =		=		⇒ α = 30o
	9		4		18		18		2

a@b: https://matematykaszkolna.pl/forum/407309.html

FischerPrise: Można by to dokładniej Wytłumaczyć? Dziękuje za poświęcony czas nad zadankiem

VII: P=0,5 d²*sinα skoro srednica okregu opisamego na tym prostokacie wynosi 6 (wiec 2R=6 ) to oznacza ze przekatna DB tego prostokatna ma dlugosc 6 Trojkat ABD jest prostokatny a srodek okrego opisanego na takim trojkacie lezy w polowie przeciwprostokatnej P=9

1
	*62*sinα=9
2

sin α= policz

a@b: 2 sposób

	1
P=		d2*sinα , d= 2R=6
	2

	1
9=18sinα ⇒ sinα=
	2

α=30^o −−kąt ostry lub α= 150^o −− kąt rozwarty

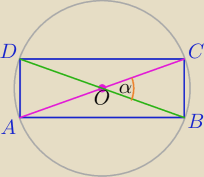Mila: |AC|=|BD|=6 |OC|=3

	1		9
PΔCOB=		*3*3sinα=		sinα
	2		2

	9
PABCD=9⇔4*		sinα=9
	2

	1
sinα=
	2

α=30^o =====

FischerPrise: Dziękuje wam wszystkim . Teraz rozumiem