Równanie, parametr Szkolniak: Treść: Dla jakich wartości m równanie (x+2)²(x−4)=m ma dokładnie dwa rozwiązania? Mam dwa tego typu zadania i w sumie nie mam bladego pojęcia jak się za to w ogóle zabrać.. mógłbym prosić o jakąś wskazówkę?

ICSP: f(x) = (x+2)²(x−4) Ekstrema: maksimum = 0 dla x = −2 minimum = −32 dla x = 2 m = 0 v m = −32 Wszystko odczytujesz z wykresu.

Szkolniak: Nie rozumiem.. Jakie ma nagle powiązanie pochodna funkcji z naszym równaniem w zadaniu?

ICSP: Aby narysować dokładny wykres potrzebujesz ekstremów. Z wykresu odczytujesz wartości parametru m. Wartości ekstremów funkcji znajdujesz dowolną metodą.

Szkolniak: Dobra, to załóżmy że obliczyłem już pochodną, oba ekstrema, to nie powinienem jeszcze w takim razie policzyć granic w ±∞? Jakby się uprzeć to w −∞ granica mogłaby być równa −3 i wtedy m=−32 by chyba odpadało? Chyba że mamy z tyłu głowy że jest to wielomian i granice w ±∞ są zawsze plus lub minus niesk.

ICSP: Naprawdę do narysowania wielomianu musisz liczyć jego granice w ±∞ Jeżeli koniecznie musisz to proszę licz. Wszystko sprowadza się do poprawnego rysunku z którego odczytasz wartości m.

pytanie: Cytując "Jakby się uprzeć to w −∞ granica mogłaby być równa −3" − z jakiej racji?

Szkolniak: Oczywiście że nie muszę.. Po prostu zastanawiam się nad tym bo nawet tego nigdy nie miałem, wiec mozliwe ze po prostu zadaje głupie pytania XD

Qulka: granice w krańcach określoności będziesz liczył przy optymalizacji żeby sprawdzić czy ekstremum lokalne jest globalnym

Szkolniak: Tak tak, takie zadania mam już za sobą, tylko po prostu to zadanie jakie tutaj wpisałem o 18:03 to nawet nigdy się z takim nie spotkałem, więc stąd takie pytania a nie inne Ale chyba nawet na maturze się takie nie pojawiały, bo kompletnie nie kojarzę

ICSP: https://matematykaszkolna.pl/strona/5342.html

Szkolniak: Hmm.. No to ja bym zrobił to w sumie tak: |x−5|=(a−1)²−4 x₁=(a−1)²+1 v x₂=9−(a−1)² I teraz: x₁+x₂>0 i x₁*x₂>0 i x₁≠x₂ i (a−1)²−4>0

Saizou : Najłatwiej graficznie, rysujesz wykres funkcji f(x) = |x−5| i przecinasz go prostymi y = (a−1)²−4.

ICSP: 1^o Dużo tych warunków (spójrz ile czasu tracisz na ich rozwiązanie) 2^o Nie myślisz: x₁ jest zawsze dodatnie. Spójrz na swoje dane wejściowe przed rozpoczęciem tworzenia warunków. Nadal jednak zostaję przy metodzie graficznej.

Saizou : Szkolniak brakuje ci najpierw założenia, że (a−1)² − 4 ≥ 0 Dopiero wówczas możesz liczyć x₁ oraz x₂

ICSP: Przecież ma to założenie

Saizou : Nie doczytałem

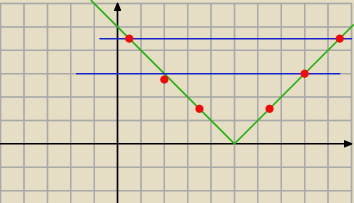
Qulka: jak widać oba dodatnie gdy 0<(a−1)²−4<5

Szkolniak: Saizou zobacz na ostatni warunek jaki napisałem + równości chyba nie dopuszczamy, wtedy otrzymujemy jedno rozwiązanie ICSP Napisałem tylko jakie warunki bym nadał i widziałem że x₁ jest zawsze dodatnie. Okej, rozumiem że graficznie byś to rozwiazął, tylko w sumie gdzie tutaj podobieństwo w tym zadaniu do zadania z początku? Tam liczyliśmy pochodną i ekstrema, a tutaj nie, więc w sumie po co mi takie zadanie?

Szkolniak: Tak naprawdę do tej pory w szkole nauczyłem się wykorzystywania pochodnej tylko i wyłącznie do wyznaczania równania stycznej do funkcji w danym punkcie + jakieś zadania optymalizacyjne, chyba nic więcej z pochodną związanego nie jest uczone teraz.

ICSP: Narysuj mi dokładny wykres funkcji f(x) = (x+2)²(x−4) bez wyznaczenia jej ekstremów. (przy czym zauważ, że to one mają największy wpływ na przecięć wykresu z prostymi poziomymi).

Szkolniak: Dooobra, rozumiem już o co chodzi.. Ciężko mi było po prostu zrozumieć po co tak naprawdę pochodną wyznaczamy i jakie to ma znaczenie razem z tym parametrem m, ale teraz wszystko jasne. Dzięki za cierpliwość i za wyjaśnienie