wykres funkcji wykładniczej anonim123:

	1
Jaki jest wykres funkcji i dlaczego taki? funkcja: e−
	x2

	1
−		jest w potędze
	x2

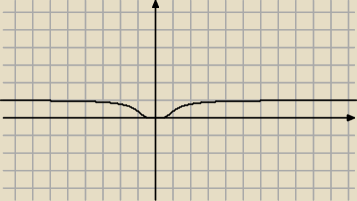
VII: x≠0 Wyznaczmy przykladowo kilka punktow

	1
x=1 y=e−1=
	e

x=2 y=e^−1/4= U{1}{e^1/4 x=3 y= e^−1/9= U{1}{e^1/9 itd x=−1 to y= e⁻¹ x=2 to y=e^−1/4 Taki jest wykres tej funkcji gdyz funkcja dana tym wzorem jest funkcja parzysta

VII: czyli f(−x)=f(x)

	1		1
f(−x)= e−		}= e−		= f(x)
	(−x)2		x2

anonim123: A dlaczego tutaj przy liczeniu asymptot pionowych jest taki wykres ten zaznaczony na niebiesko w czym ma mi on pomóc? https://zapodaj.net/ee6af504206c5.jpg.html

Jerzy: D = R\{0}

	1
f(x) =
	e1/x2

	1
limx→0+ = [		] = 0
	∞

	1		1
limx→∞ = [		] = [		] = 1
	e0		1

Jerzy: Przecież na tym zdjęciu jest inna funkcja.

anonim123: Wiem że inna ale myślałam że jak poznam wykres tej z pierwszego postu to to zrozumiem. A jak mam zrozumieć przykład z 12:54?

krzysiu: Musisz policzyć granice przy x−>±∞, a później pochodną żeby sprawdzić czy są ekstrema

anonim123:

	1
A dlaczego granica z e do −		jest równa zero?
	x2

anonim123: zbiegająca do zera z lewej strony?

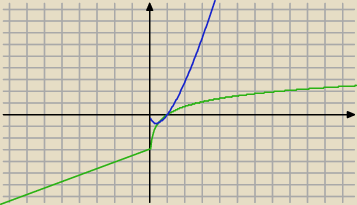
Jerzy: Odpowiem przykładem: Zielona , to f(x) = lnx Niebieska, to g(x) = 2x*lnx Czy znając wykres f(x) = lnx , da się odgadnąć jak wygląda wykres funkcji g(x) ? Edytor rysunku niestety nieco zepsuł wykres zielony, ale myślę,ze wiesz jaki jest wykres funkcji: f(x) = lnx

Jerzy: Czy rozumiesz, co napisałem o 12:56 ? Tam masz odpowiedź dlaczego.

Jerzy: Skoro funkcja jest parzysta, to : lim_x→0⁺ = lim_x→0⁻

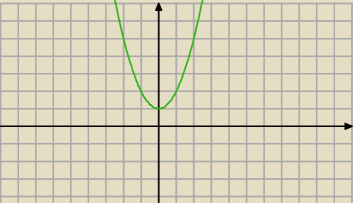
Jerzy: To jest funkcja parzysta. Ile wynosi: lim_x→0⁺ , a ile : lim_x→0⁻ ?

anonim123: To będzie 1 obustronna 13:20?

Jerzy: No jasne. Dlatego o 12:56 liczyłem tylko jednostronne granice, bo funkcja jest parzysta i to co się dzieje na prawo od osi OY, dzieje się na lewo od niej.

anonim123: Dziękuję