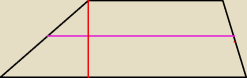
 Dlaczego prosta poprowadzona przez środki boków w trapezie
ZAWSZE dzieli jego wyskokość na pół? Jaki jest tego dowód albo twierdzenie, czy własność?
Dlaczego prosta poprowadzona przez środki boków w trapezie
ZAWSZE dzieli jego wyskokość na pół? Jaki jest tego dowód albo twierdzenie, czy własność?
 )
)
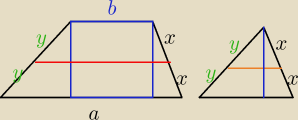 wycinasz niebieski
mały trójkąt o bokach x,y,pom jest podobny do 2x,2y,(a−b) (cecha bkb) w skali 1/2
więc pomarańczowa jest równoległa do podstawy (przy okazji równa (a−b)/2 dlatego potem jak
dodasz b (niebieskie) to ta środkowa będzie (a+b)/2
no i skoro skala jest 1/2 to małe h = 1/2 całej wysokości
wycinasz niebieski
mały trójkąt o bokach x,y,pom jest podobny do 2x,2y,(a−b) (cecha bkb) w skali 1/2
więc pomarańczowa jest równoległa do podstawy (przy okazji równa (a−b)/2 dlatego potem jak
dodasz b (niebieskie) to ta środkowa będzie (a+b)/2
no i skoro skala jest 1/2 to małe h = 1/2 całej wysokości
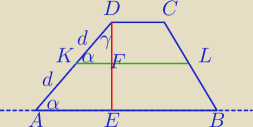 1)
ΔKFD∼ΔAED cecha kkk
1)
ΔKFD∼ΔAED cecha kkk
| KD | AD | ||
= | ⇔ | ||
| DF | DE |
| d | 2d | 1 | |||
= | ⇔|DF|= | |DE| | |||
| DF | DE | 2 |
| DF | FE | ||
= | ⇔ | ||
| KD | AK |
| DF | |FE| | ||
= | ⇔ | ||
| d | d |
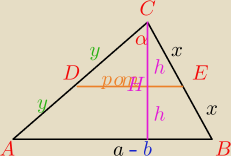 ΔDEC ~ ΔABC bo y/2y=1/2 oraz x/2x =1/2 oraz α=α cecha bkb
zatem h/H=1/2 czyli H=2h
ΔDEC ~ ΔABC bo y/2y=1/2 oraz x/2x =1/2 oraz α=α cecha bkb
zatem h/H=1/2 czyli H=2h
 ! <3
! <3