liczby zespolone janek: Znajdź współrzędne punktu P',który otrzymamy w wyniku obrotu puntu P=(2,−1) wokół początku układu współrzędnych o kat alfa=240. Wykonać także rysunek.

VII: https://matematykaszkolna.pl/strona/896.html

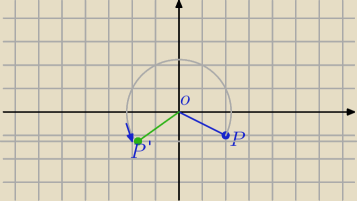
Mila: 240^o=180^o+60^o P=(2,−1) x'=xcosα−ysinα y'=xsinα+ycosα x'=2*cos(180+60^o)+sin(180+60^o)

	1		√3		√3
x'=2*(−		)−		=−1−
	2		2		2

	√3		1		1
y'=2*(−		)+		=−√3+
	2		2		2

Maciess: W temacie jest coś o zespolonych więc może też wstawie. Utożsamimy na chwile R² z zespolonymi. Niech z=2−i Ze wzoru de Moivre'a wiemy, że przy mnożeniu liczb zespolonych moduły się mnożą, a argumenty dodają. Więc obrót to nic innego jak pomnożenie liczby przez liczbe zespolona o module 1 i ustalonym kącie.

	1
W tym wypadku u=cos(240o)+isin(240o)=−		(1+√3i).
	2

	1		2+√3		2√3−1
Mnożymy z*u=−(2−i)*		(1+√3i)=		+i*
	2		−2		−2

	2+√3		2√3−1
I wracając do R2 mamy P'=(		,		)
	−2		−2