To będzie przed ostatnie zadanie;) FischerPrise: W pewnym czworokącie wypukłym przekątne sa jednocześnie dwusiecznymi kątów wewnętrznych Zatem czworokąt ten jest: deltoidem prostokątem rombem trapezem Proszę o wyjaśnienie

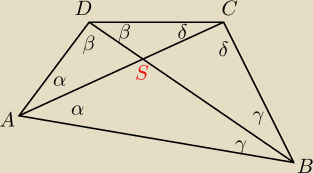
Godzio: 2α + 2β + 2γ + 2δ = 360^o α + β + γ + δ = 180^o β + γ + 2δ = 180^o ⇒ β + γ = 180^o − 2δ, wstawiam to do równania powyżej: α + 180^o − 2δ + δ = 180^o ⇒ α − δ = 0 ⇒ α = δ, a zatem trójkąt ACD jest równoramienny: |AD| = |DC| Analogicznie pokazujemy równość pozostałych boków, stąd γ = β Wracając do naszego równania α + β + γ + δ = 180^o mamy: 2α + 2β = 180^o ⇒ α + β = 90^o ⇒ ∡ASD = 90^o Czworokąt o równych bokach i przekątnych przecinających się pod kątem prostym to romb