optymalizacja Khazix66: W okrag o promieniu r jest wpisany trojkat rownoramienny o kacie α miedzy bokami rownej dlugosci. Wyznacz kat α dla ktorego pole powierzchni trojkata osiaga maksimum.

kerajs:

	π
α=
	3

Khazix66: hej kerajs moglbys pokazac mi jak to rozwiazac?

kerajs: Wiadomo, że maksimum nie będzie dla kąta z przedziału (90^o;180^o) . / gdyż zmniejszając kąt od 180^o do 90^o to zarówno podstawa, jak i wysokość (do niej prostopadła) rosną, więc i pole trójkąta rośnie / Szukane maksimum będzie w przedziale (0^o;90^o> Dzielę trójkąt na trzy trójkąty w których dwa boki są promieniami okręgu, a wtedy:

	1		1		1
P(α)=		R2 sin (180o−α) +		R2 sin (180o−α) +		R2 sin (2α)
	2		2		2

P(α)=R² sin α (1+cos α) Znajdź ekstremum z P(α).

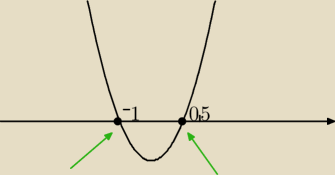Khazix66: Obliczyłem wyszło mi ze P'(α)=R²cos²α+R²cosα−R² i jak przyrownalem do 0 to wychodzi ze cosα=−1 ale to odpada bo cosα=−1 dla α=180, no i zostaje dla α=60, ale jak narysowalem taki

	1
wykres jak wyzej, to z niego wynika, że max jest w −1 a minimium w		ktos mi powie
	2

	1
dlaczego? bo w		pochodna zmienia znak −/+ czyli tam jest minimum lokalne? Prosze o
	2

wyjasnienie

Khazix66: Zgubilem 2, tam powinnobyc 2R²cos²α

Godzio: Rysowanie takiego wykresu dla funkcji trygonometrycznej jest niebezpieczne. Ekstrema w takich wątpliwych przypadkach lepiej weryfikować bazując na 2 pochodnej. Pozwolę sobie nieco uprościć Twój zapis: P'(α) = R²(2cos²(α) − 1 + cos(α)) = R²(cos(2α) + cos(α)) P''(α) = R²(−2sin(2α) − sin(α)) Jeżeli P''(α₀) > 0 mamy minimum, jeśli P''(α₀) < 0 mamy maksimum:

	π		2π		π
P(		) = R2(−2sin(		) − sin(		) = −R2 * √3 < 0 dla R ≠ 0 (a to wiemy)
	3		3		3

	π
Konkluzja − w		istnieje maksimum.
	3

Nawiązując do Twojego rozwiązania. Wynika z niego, że niezależnie od R, funkcja jest rosnąca od 0.5 do ∞, czy aby na pewno tak jest skoro cosinus / sinus jest funkcją okresową?

a@b: Godzio

Godzio: No witam Wzięło mnie coś dzisiaj

a@b: Co u Ciebie? jeżeli można?

Mila: P(α)=R² sin α (1+cos α), α∊(0,π) P'(α)=R²*( cos²α−sin²α+cosα) ( cos²α−sin²α+cosα)=0 2cos²α+cosα−1=0 cosα=t , |t|<1 2t²+t−1=0 Δ=9

	1		1
t=−1 lub t=		⇔(t+1)*(t−		)=0
	2		3

	1		1
(cosα+1)*(cosα−		)>0⇔ cosα>		⇔
	2		2

	π
α∊(0,		)
	3

	π
w α=		pochodna zmienia znak z (+) na (−)
	3

	π
P(α) ma maksimum dla α=
	3

	√3		1		3√3R2
Pmax=R2*		*(		+1)=
	2		2		4

Godzio: Oczywiście, że można Czas zaczął przyspieszać, niedawno jeszcze liceum, a zaraz 30 Wciąż wykładam na polibudzie, mam właśnie serie kolokwiów, i jakieś 200 prac do sprawdzenia, jestem załamany co niektórzy potrafią pisać mimo, że zdali maturę Miło czasem tu wejść i przypomnieć sobie co nieco, rozruszać umysł. Generalnie mogę powiedzieć, że już jestem spełniony, mogę iść na emeryturę, dołączę do Ciebie! A u Ciebie jak? Dalej zajadasz się chałwą i grywasz w brydża?

Mila: Witaj Godzio, tak dawno tu nie zaglądałeś Dziś prawdziwych licealistów już nie ma! Czy to pandemia , czy wartości liberalne tak sprawiły? Miło czytać, że Twoja kariera przebiega zgodnie z marzeniami. Powodzenia

Godzio: Mało czasu niestety Mila, teraz studenci mają znacznie lepiej, bo to ja im rozwiązuje wszystkie zadania, więc mają mnóstwo przykładów rozwiązanych od A do Z z pełnym wytłumaczeniem, tylko korzystać. Sami muszą coś robić w domu oczywiście, ale jak przychodzi co do czego to już różnie bywa.

Khazix66:

	π
Mila a skad widac ze dla α=		pochodna zmienia znak z + na −?
	3

Mila:

	1		1
Z nierówności (cosα+1)*(cosα−		) >0⇔(cosα−		)>0 i x∊(0,π)
	2		2

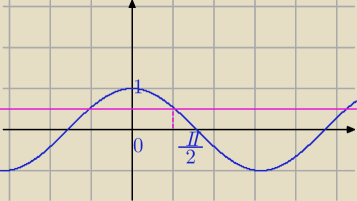
	π		1
Na wykresie masz , że dla x∊(0,		) funkcja cosx>		w tym przedziale
	3		2

	1		π
cosα<		) dla x∊(		,π)
	2		3

Przemyśl to, wiem, że się plącze . Może licz drugą pochodną jak radzi Godzio, to unikniesz pomyłki.