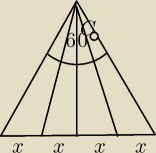
 Czy jeśli w trójkącie równobocznym (każdy kąt po 60 stopni) podzielę odcinek leżący naprzeciwko
kąta na 4 równe części i połączę punkty podziału z wierzchołkiem to na tej podstawie mogę
stwierdzić, że utworzone kąty będą miały miarę po 15 stopni?
Będę ogromnie wdzięczny za jakieś uzasadnienie.
Czy jeśli w trójkącie równobocznym (każdy kąt po 60 stopni) podzielę odcinek leżący naprzeciwko
kąta na 4 równe części i połączę punkty podziału z wierzchołkiem to na tej podstawie mogę
stwierdzić, że utworzone kąty będą miały miarę po 15 stopni?
Będę ogromnie wdzięczny za jakieś uzasadnienie.
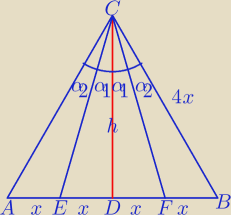 Możesz wykazać, że α1≠α2
Możesz wykazać, że α1≠α2
| 4x√3 | ||
h= | =2x√3 | |
| 2 |
| 2x√3 | 2√3 | |||
cosα1= | = | |||
| x√13 | √13 |
| 7 | ||
cosα2= | ||
| 2√13 |
