geometria analityczna, optymalizacyjne z wykorzystaniem pochodnej Maciek: Jeden z boków kwadratu o wierzchołkach A i B zawiera się w prostej y=¹₂x , a wierzchołek C należy do wykresu funkcji y=−⁸_x . Wiedząc, że kwadrat ten ma najmniejsze możliwe pole powierzchni, oblicz długość jego przekątnej.

janek191:

	8
d =
	√5

p = d √2 = 1,6 √10 ================

Maciek: Skąd wzięły się te liczby? Jak określić d?

janek191:

	8
C = ( x, −		)
	x

x − 2 y = 0

	16   I x + I   x
d =
	√5

	16
d1(x) = x +
	x

	16
d1'(x) = 1 −		= 0 ⇔ x = − 4 lub x = 4
	x2

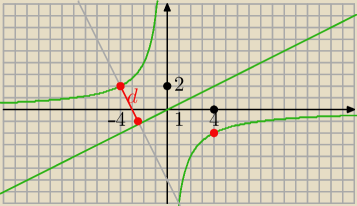
więc C = ( −4, 2) lub C= ( 4, 2) oraz

	I − 4 − 4 I		8
d =		=
	√5		√5

p = d√2 = 1,6 √10 ==================

Maciek: Okej, dziękuję. Rozumiem, że najmniejsze pole będzie wtedy, gdy będzie najmniejsza odległość punktu na krzywej od prostej, czyli w punkcie o odciętych −4 oraz 4.

janek191: