pomocy karolekkk27: Zad 1. Udowodnij ze dla kazdej ujemnej liczby rzeczywistej x prawdziwa jest nierownosc

	x		4		4
		+		≤−
	9		x		3

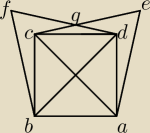
Zad 2. Dany jest kwadrat ABCD. Zbudowano trojkaty rownoboczne ACE i BDF tak ze wierzcholek D kwadratu lezy wewnatrz trojkata ACE a wierzchiolek C wewnatrz trojkata BDF. Odcinki CE i DF przecinaja sie w punkcie G. Wykaz ze CG=CF. Zad 3. Punkty A=(3,1) i B=(6,5) sa wierzcholkami trojkata prostokatnego w ktorym BAC=90. Wierzcholek C tego trojkata lezy na osi Oy ukladu wspolrzednych. Wyznacz wspolrzedne wierzcholka C. Nie wiem jak dac duze litery do wierzcholkow na rysunku, probowalem 3 zadanie robic z twierdzenia pitagorasa ale cos sie zamieszalem pomoze ktos?

chichi: Widzę, połowa zadań z arkusza nowej ery styczeń 2021 (1) x<0

x		4		4
	+		≤−		/ *9x
9		x		3

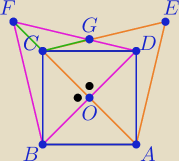
x²+36≥−12x ⇒ x²+12x+36≥0 ⇒ (x+6)²≥0 Q.E.D. (2) |∡CFG|=30^o ∧ |∡ECO|=60^o ∧ |∡FCG|=180^o−|∡ECO|=180^o−60^o=120^o |∡FGC|=180^o−120^o−30^o=30^o ⇒ |∡FGC|=|∡CFG|=30^o ⇒ |CF|=|CG| (3) Niech C=(0, y) → →

	13		13
AB o AC = [3, 4] o [−3, y−1] = 0 ⇒ −9+4y−4=0 ⇒ y=		⇒ C=(0,		)
	4		4

P.S. Wielkie litery na rysunku tworzy się SHIFT + litera

karolekkk27: dzieki te 2 pierwsze rozumiem ale tego 3 nie o co tma chodzi?

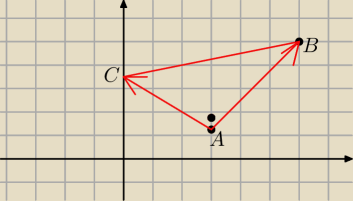
VII: na to aby wektory AB i AC byly prostopadle potrzeba aby ich iloczyn skalrny wynosil 0

VII: Mozesz to zadanie zrobic tez tak

	5−1		4
napisac wspolczynnik kierunkowy prostej AB m=		=
	6−3		3

napisac rownanie prostej prostopadlej do AB i przechodzacej przez punkt A (czyli prostej AC

	3
m1=−
	4

y=m₁(x−3)+1

	3		3		13
y=−		(x−3)+1= −		x+
	4		4		4

y=ax+b ogolnie wspolczynnik b wskazuje punkt przeciecia wykresu funkcji liniowej z osia OY

	13
w zwiazku z tym C=(0,		)
	4

karolekkk27: okej dzieki VII poprawilem swoje obliczenia w tym sposobie z twierdzeniem pitagorasa i tez mam

	13
ze C=(0,		)
	4