Planimetria
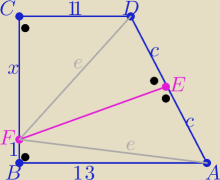
Alaias: Podstawy trapezu prostokątnego ABCD mają długości AB=13, CD=11 i bok BC jest prostopadły do
podstawy AB.
Symetralna boku AD przecięła ramię AD w punkcie E, a ramię BC w punkcie F, takim, że BF=1.
Oblicz pole trapezu ABCD.
23 sty 17:10
ite: Symetralna boku AD przecięła ramię AD? nie ma błędu?
23 sty 17:32
Alaias: Nie ma błędu − ramię ( bok AD ) jego symetralna przecina w punkcie E , a drugie ramię BC w
punkcie F
23 sty 17:47
a@b:
e
2=13
2+1
2 =170
x
2=170−11
2
x=7
to h=8
P= ..........=96
23 sty 18:05
chichi:
P=96 potwierdzam
23 sty 18:07
a@b:
Coś TY ?
23 sty 18:08
chichi:
23 sty 18:10
a@b:
23 sty 18:10
Alaias: Dzięki
23 sty 19:11
BoosterXS: Skąd wiadomo, że odcinki AF i DF są równej długości?
28 sty 21:30
BoosterXS: Nie było pytania, już to widzę
28 sty 21:32
chichi:
ΔAEF≡ΔFED (cecha bkb) − (c−900−|FE|)
28 sty 21:33