Kochani jak obliczyć to zadanie? Kate : Graniastosłup prawidłowy czworokątny, którego krawędź podstawy ma długość 20 cm a wysokość 24 cm, przecięto płaszczyzną przechodzącą przez przekątną podstawy i nachyloną do płaszczyzny podstawy pod kątem 60°. Oblicz pole przekroju.

chichi: Najpierw sprawdź jaka figura będzie przekrojem, później skorzystaj z podobieństwa i z górki do rozwiązania

Beti : nie umiem tego zadania zrobić

chichi: To w końcu Kate czy Beti?

Kate: zadanie moje moze Beti też nie umie

Beti : nie jestem w stanie pomóc w rozwiązaniu

Kate : szkoda

Kate : pomoże ktoś?

chichi:

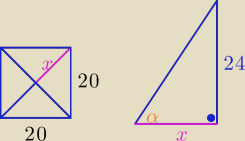
	20√2		24		24		6√2
x=		=10√2, tan(α)=		=		=		, tan(60°)=√3
	2		x		10√2		5

	6√2
√3>		tangens jest funkcją rosnąca na całej swojej dziedzinie ⇒ 60°>α
	5

Kate : wielkie dzięki

chichi: α≈59.5°

Kate : dzięki

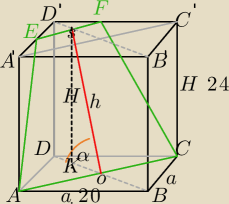
Mila: a=20, H=24,α=60^o 1) Sprawdzamy kąt nachylenia ACD' do płaszczyzny podstawy (Dorysuj sobie na osobnym rysunku, nie chcę zamazać ilustracji)

	1
|DO|=		*20√2=10√2
	2

	H		24		24√2		6√2
tg∡DOD'=		=		=		=
	|DO|		10√2		20		5

Porównanie :

6√2
	i √3 /2
5

36*2		72		22
	=		=2		<3
25		25		25

Przekrój jest trapezem. 2) W ΔSKO: |AC|=20√2

	H		√3		24
sin60o=		⇔		=		⇔√3*h=48 /*√3
	h		2		h

h=16√3

	|KO|		1		|KO|
cos60=		⇔		=		⇔
	h		2		16√3

|KO|=8√3 |DK|=10√2−8√3=|D'S| |EF|=2|D'S|=20√2−16√3

	20√2−16√3+20√2
3) PACFE=		*16√3
	2

P_ACFE=(20√2−8√3)*16√3=320√6−384 P_ACFE=64*(5√6−6)

Kate : bardzo dziękuję za pomoc

Mila: Sprawdź rachunki