Policz objętość bryły za pomocą całki podwójnej ograniczonej powierzchniami Lukasz: Policz objętość bryły za pomocą całki podwójnej ograniczonej powierzchniami z=−1−√x²+y² x²+y²=2x i płaszczyzna z=0 Mam rysunek, jest to walec który jest ograniczony płaszczyzna z=0 i z dołu paraboloida (nie wiem czy dokładnie tak się nazywa ta figura przestrzenna, No nie ważne taka lotka w dół powiedzmy) z=−1−√x²+y² No i ograniczenia jakie teraz mam dać D? Do tego jeszcze te wsp biegunowe... bo ta bryla jest przecież ograniczona przez promień walca i wysokość z góry i dołu różnymi funkcjami. Ktoś podsunie pomysł ? 😥

Lukasz: Myślałem coś nad tym ze jest ona ograniczona przez −1−√x²+y² ≤ z ≤ 0 i 0≤2cosφ No ale nie jestem pewien i nie wiem jak zamienić granice z na wsp biegunowe

jc: Zapomnij o całkach. Stożek o nachyleniu tworzącej = 45^o przecinamy walcem (x−1)²+y²=1. Pole = √2 * π.

Lukasz: A do tego zapomniałem ze jedna z ograniczeń musi być wartością a druga jakaś funkcja

Lukasz: @jc muszę całka bo to zadania na egzaminy

Lukasz: Poza tym to nie jest to pole które szukamy chyba Bo ty chyba policzyłeś „czapkę” tej paraboloidy choć mogę się mylić

jc: Oj, liczymy objętość. Odbij do góry, będzie ładniej. x= r cos φ y =r sin φ J= r −π/4 ≤ φ ≤ π/4 0 ≤ r ≤ 2 cos φ V = ∫dφ ∫ (1+r)r dr (dopisz odpowiednie granice całkowania)

Lukasz: Prawie tak jak w rozw tylko nie od pi/4 tylko od pi2 do −pi/2 i właściwie to czemu takie granice ? Nie powinnismy rozpatrywać całki na całym okręgu czyli od 0 do 2pi? I skąd jest( 1+r)

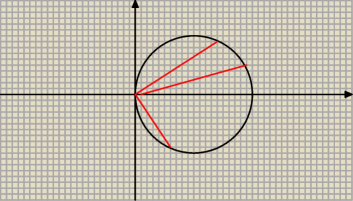
jc: Dobrze piszesz, od −π/2 do π/2. 0 ≤ r ≤ 2 cos φ [−π/2, π/2] to największy przedział na którym kosinus jest nieujemny. 1+√x²+y² = 1+r², a to r przed dr to jakobian.

Lukasz: Sory, że tak odkopuje, ale teraz pomyślałem że przeciał dla kąta jest zrozumiały jak jest koło w 1 lub 4 ćwiartce. Wtedy tylko cos jest dodatni. A gdyby był w 2 i 3 ćwiartce, gdzie nie ma funkcji dodatniej jednocześnie w obu tych ćwiartkach?

Lukasz: + jeszcze 1 pytatnie. Podany przez @jc wzór ∫∫1+√x²+y² no to czemu całkujemy po czymś takim? po 1. wzór na pole to √1+fx²+fy² przy czym fx to pochodna czastkowa funkcji którą całkujemy. A my całkujemy x²+y²=2x no bo to walec jest ograniczony. Poza tym, gdyby nawet było takie równanie jak podał @jc to przecież taki walec nie jest w ogóle ograniczony przez płaszczyznę z=0

Lukasz: Ok, trochę się pomyliłem, bo liczymy objętość a nie pole, więc cofam zdanie dot. wzoru. Ale dalej, czemu jest 1+√x²+y²