Algebra w przestrzeni: wyznaczanie równania ogólnego płaszczyzny Nieznajomy_23: Ktoś sprawdzi? Napisz równanie ogólne płaszczyzny, która: 1) jest równoległa do osi Ox i zawiera punkty M = (1,−1,−3) i P = (−5,4,−2) π: Ax + By + Cz +D = 0 wektor MP = [−6,5,1] wektor x = [1,0,0] wektor normalny n = [A,B,C] = [−6,5,1] x [1,0,0] = [0,1,−5] π: 0x+y−5z+D = 0 => π: y−5z−14 = 0 M = (x,y,z) = (1,−1,−3) −1+15 + D = 0 D = −14 2) zawiera punkt M = (2,7,−3) oraz prostą x = 2t, y = t − 1, z = −t + 2 wektor v = [A,B,C] = [2,1,−1] punkt M = (2,7,−3) = (x0,y0,z0) π: A(x−x0)+B(y−y0)+C(z−z0) = 0 2(x−2)+1(y−7)−1(z+3) = 0 2x−4+y−7−z−3 = 0 π: 2x+y−z−14 = 0

	⎧	x = 4t − 1
3) zawiera prostą l :	⎨	y = −3t −1
	⎩	z = t

	⎧	x = 4t − 2
i jest równoległa do prostej k:	⎨	y = 3t + 3
	⎩	z = 2t

Wektor kierunkowy prostej l: L = [4−3,1] Wektor kierunkowy prostej k: K = [4,3,2] Wektor normalny do szukanej płaszczyzny π: n = [A,B,C] = K x L = [4,3,2] x [4,−3,1] = [9,4,−24] π: 9x+4y−24z+D = 0 => π: 9x+4y−24z+13 = 0 P = (−1,−1,0) −9−4+D = 0 D = 13

jc: (1) ok

Nieznajomy_23: a jak wygląda sytuacja z 2) i 3)?

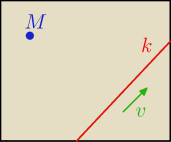
luui: (2) Czy wektor v jest wektorem normalnym szukanej płaszczyzny? // spójrz na rysunek (czarny prostokąt reprezentuje płaszczyznę) (3)

Nieznajomy_23: @luui z rysunku twojego wynika, że nie jest.

Nieznajomy_23: tylko nwm jak to zrobić inaczej

Jerzy: 2) v to wektor kierunkowy prostej. Wybierz dowolny punkt P na prostej. Wektor normalny szukanej płaszczyzny, to :v x PM^→

luui: Znajdź punkt na prostej, połącz go z punktem M to otrzymasz wektor u. n = u x v // wektor normalny

Nieznajomy_23: czyli: M = (2,7,−3) P = (1,1,1) wektor PM = [−1,−6,4] wektor kierunkowy v = [2,1,−1] wektor normalny n szukanej płaszczyzny: n = v x PM = [2,1,−1] x [−1,−6,4] = [−2,−7,−11] ?

Nieznajomy_23: pomyliłem się w liczeniu wektor PM. PM = [1,6,−4] n = v x PM = [2,7,11]

luui: Ten punkt nie należy do prostej, podstaw, np t=0 to otrzymasz P=(0,−1,2)

Jerzy: Punkt P = (1,1,1 ) nie należy do tej prostej.

luui: 1:1 Jerzy

Nieznajomy_23: aha, tak to się robi. Więc: P = (0,−1,2) M = (2,7,−3) wektor PM = [2,8,−5] wektor v = [2,1,−1] wektor normalny n = [2,1,−1] x [2,8,−5] = [3,8,14] π: Ax + By + Cz +D = 0 3x+8y+14z+D = 0 I podstawiam punkt M = (2,7,−3) 6+56−42+D = 0 D = −20 π: 3x+8y+14z−20 = 0

Nieznajomy_23: Teraz jest dobrze?

luui: ok

Nieznajomy_23: dzięki za pomoc