Problem matematyczny Siemka: zacząłem się uczyć do matury i ogólnie nic nie umiem no to staram się wszystko fajnie pojąć nawet fajnie mi to idzie bo dzisiaj sobie zacząłem no i se ogarniam funkcje kwadratowe i wiem jak te miejsca zerowe i w ogóle porobić wykresy wszystko fajnie, Ale staram się zrozumieć te postacie iloczynowe ogólne i kanoniczne no i mam problem taki że ktoś mógłby mi to wyjaśnić bo nie wiem jak pewną rzecz ogarnąć Mianowicie chodzi o to że mam swoją wymyśloną postać iloczynową (x−2)(x−2) z góry założyłem, że ma w niej być 1 rozwiązanie. Potem zmieniłem sobie ją na postać ogólną x²−4x+4 Delta wychodzi 0 więc jest git. No i o co chodzi z tym = sie Bo np =0 to łatwo zrobić bo jak się podstawia to jest tak samo do tych 2 postaci. ale jak już chce żeby było =4 To coś jest nie halo, w postaci ogólnej wychodzi że x to 6 no bo 6−2 to 4 A jak podstawię pod postać iloczynową to równanie wychodzi 8 no bo 6²−4*6+4=36−28=8 A jak to wklepę w internet to w ogóle kosmos. A jak licze se np rózne nawiasy to mi matemaks mowi zeby se brac jeden i liczyc potem drugi i jest gitara to czemu tutaj jest cos nie tak. Może mi to ktoś jakoś wytłumaczyć? Mi się wydaje, że coś źle licze a ze nie mam wiedzy to nie wiem co

Qulka: jak chcesz by było równe zero to wszystko na jedną stronę

Siemka: Ja chce żeby to było równe 4 Tylko nie wiem czy tak w ogóle można i o to mi właśnie chodzi

Siemka: Bo ja chyba tu czegoś nie rozumiem

Qulka: no chyba nie

Siemka: Czyli równania kwadratowe zawsze sprowadzają sie do =0 tak? Oprócz kanonicznych?

VII: y=(x−2)(x−2)= (x−2)² To jest postac kanoniczna wiadomo ze z tej postaci Δ=0 (bo to wzor skroconego mnozenia Jesli ma sie to rownac 4 to piszesz (x−2)²=4 x²−4x+4=4 x²−4x+4−4=0 x²−4x=0 (masz rownanie kwadratowe niezupelne x(x−4)=0 stad x=0 lub x−4=0 to x=4

Jerzy: Ochłoń. 1) (x−2)(x−2) = 0 ⇔ x=2 2) (x−2)(x−2) = 4 ⇔ x² − 4x + 4 = 4 ⇔ x² − 4x =0 ⇔ x(x−4) = 0 ⇔ x = 0 lub x = 4

Siemka: To sie ma równać 4 ale nie x=4 tylko równanie ma wyjść 4 po podstawieniu x. w postaci ogólnej podstawiam pod x 6 i wychodzi dobrze a w postaci ogólnej nie.

VII: (x−2)²=4 podstaw za x=0 i potem za x=4 i sprawdz czy to rowna sie 4

Siemka: Ale to jest postać kanoniczna a mi chodzi o to (x−2)(x−2)=4 No i Słyszałem, że trzeba obliczać nawiasy po kolei czyli x−2=4 i x−2=4 Czyli wyjdzie x 6. I teraz widząc postać kanoniczną widzę, że coś jest nie tak. A więc co trzeba robić w przypadku postaci iloczynowej żeby wyszło dobrze bo nie chce w przyszłości popełniać błędów.

Qulka: nawiasy po kolei to tylko jak =0 bo wystarczy że jakikolwiek nawias jest zerem i całość mnożenia jest zero

Qulka: bo to z reguły że A•B•C•D=0 gdy albo A=0 albo B=0 albo C=0 albo D=0

Siemka: A okey to wiele wyjaśnia. z tym że tylko jak jest =0 zapamiętam to.

Qulka: ale jeśli chcesz by A•B=4 to może być A=1B=4 albo A=2 B=2 albo A=1/2 B=8 więc już nie działa jeśli (x−2)(x−2)=4 to zapisz (x−2)²=4 więc x−2 =2 lub x−2=−2 i licz

Siemka: w postaci kanonicznej jest łatwiej :C a jak będę miał postać ogólną i zamiast =0 to np =4 to przerzucam to 4 na lewą stronę i daje dalej =0 i sobie liczę ?

Qulka: tak

Siemka: Dobra dzięki za informacje będę sobie kombinował dalej

VII: tak Z postaci kanonicznej nie odzytasz besposrednio miejsc zerowych funkcji tylko wsporzedne wierzcholka paraboli

Siemka: Czyli w tych równaniach zawsze sie szuka miejsc zerowych i wierzchołków?

Qulka: nie.. ale dlatego jest tyle postaci że każda pokazuje coś innego

Qulka: no i na maturze to rzeczywiście najczęściej miejsca zerowe lub wierzchołek

Siemka: No oby bo wtedy tylko te wzory na q p x1 x2 i jest latwo. A jak jest ta delta =0 To cytuje "To jest postac kanoniczna wiadomo ze z tej postaci Δ=0 (bo to wzor skroconego mnozenia Jesli ma sie to rownac 4 to piszesz (x−2)2=4 x2−4x+4=4 x2−4x+4−4=0 x2−4x=0 (masz rownanie kwadratowe niezupelne x(x−4)=0 stad x=0 lub x−4=0 to x=4" Dlaczego tutaj są 2 rozwiązania? ta delta tyczy się tylko miejsc zerowych?

Qulka: delta to taka pomocnicze wyrażenie żeby ułatwić zapis

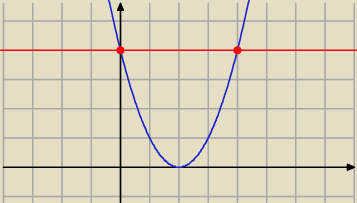
Qulka: narysuj sobie to równanko (x−2)² to niebieska linia =4 to czerwona i przecinają się w dwóch miejscach ... więc dwa rozwiązania

Siemka: Czyli delta nie powinna byc rowna 0 bo jak jest 0 to znaczy że jest jedno.

VII: Myslaem iz sie rozumiemy Postac kanoniczna jest taka y=a(x−p)²+q y=(x−2)² zuwaz ze tutaj q=0 i wtedy Δ=0 wiec jaka kolwiek wstawisz liczbe za p to dostajesz wzor skroconego mnozenia np (x−5)²= x²−10x+25 z tego delta Δ=100−4*25=0 (x+8)²= x²+16x+64 Δ=16²−4*64=256−256=0

Qulka: gdyby było =0 to ta czarna na dole to przecina się w jednym miejscu więc jedno rozwiązanie

Siemka: Czyli z zapisu (x−2)²=4 muszę obliczyć postać ogólną i dopiero potem liczę deltę i wtedy wyjdzie, że sa 2 rozwiązania tak?

a@b: (x−2)²=4 x−2=2 lub x−2= −2 x=4 lub x=0

a@b: A teraz rozwiąż: (x+3)²=16

Qulka: nie musisz.. lepiej myśleć jak zrobić prościej.. ale jak nic nie umiesz to to jest dobra metoda, bo uniwersalna

Siemka: Ja wiem jak to rozwiazac. Chodzi mi o tą deltę ona się zmienia w zalezności od tego co jest po = tak? Co do (x+3)²=16 to będzie x =1

a@b: x=1 lub x= −7 dwa rozwiązania

Qulka: (−4)² też =16

Siemka: Aha dobra wiem jak to się robi x+3=4 przesuwam 3 na prawa i mam x=4−3 x=1 x+3=−4 przesuwam se na prawą i mam x−−7 Dobra ide spać jutro się jeszcze pouczę będzie dobrze.

a@b:

Filip: Zacząłeś się uczyć do matury w pierwszej liceum? Trochę wcześnie, ale lepiej późno niż wcale

Siemka: nie no wlasnie matura w tym roku to sie ucze xd

Mila: Siemka , czarno widzę wyniki tej matury, jeżeli nie zabierzesz się do pracy (x+3)²=16 ⇔ x+3=4 lub x+3=−4 x=1 lub x=−7