Korzystając ze wzoru Cauch'ego lub jego uogólnienia oblicz całkę Lukasz: Korzystając ze wzoru Cauch'ego lub jego uogólnienia oblicz całkę

	ezdz
∮
	z(z−2i)

gdzie C jest krzywą o równaniu |z−3i|=2 zorientowaną dodatnio. Hej. Mam takie o to zadanie do rozwiązania. Wziąłem to z egzaminu, ktorego jeszcze nie miałem. Jest ktoś kto rozumie to i chciałby mi wytłumaczyć jak to rozwiązywać? Ogólnie jak próbowałem znaleźć coś w internecie to albo źle podchodze do tych tematów (za mało abstrakcyjnie) albo jest mocnym językiem napisane. Nic kompletnie nic nie rozumiem co jest napisane na stronach. Już się pogodziłem z tym że może nie zrozumiem tego w sposób logiczny, czym to wgl jest ale może zapamiętam jakiś schemat Pozdrawiam PS: tu wstawiam rozwiazanie jakby ktoś potrzebował: ∫U{f(z)dz}{{(z−z0)}=2πif(z0)

	ez   z		ez
∫		dz=2πi		=
	z−2i		z

	e2i
=2πi		=πe2i=π(cos2+isin2)
	2i

ICSP:

	f(z)
∫		= 2πif(z0)
	z − z0

zapomniałeś o najważniejszym. Czym jest tutaj z₀? Jaki ma on związek z obszarem po którym całkujesz?

Lukasz: @ICSP środkiem tego obszaru? szczerze nie mam pojęcia, nie potrafię zrozumieć za chiny tego tematu

ICSP: Masz pewien obszar (zbiór otwarty i spójny) D a wewnątrz niego pewną krzywą Jordana γ (np okrąg) Wtedy dla wszystkich punktów z₀ które leżą wewnątrz tej krzywej zachodzi wzór:

	f(z)
∫y		dz = 2πi f(z0)
	z − z0

Dlaczego ten wzór jest taki istotny? Zapewne wiesz, że całka po krzywej Jordana z funkcji analitycznej jest równa 0. Problem pojawia się jeśli nasza funkcja ma punkt osobliwy wewnątrz krzywej γ. W takim przypadku używasz właśnie tego wzoru. Masz swoją krzywą: |z − 3i| = 2 Patrzysz które punkty osobliwe (najprościej powiedzieć, ze są to miejsca zerowe mianownika) wpadają do obszaru wewnątrz tej krzywej. Następnie dla tych miejsc zerowych stosujesz ten wzór.

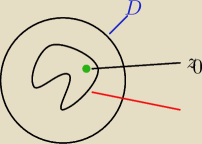
Lukasz: Ogólnie to mniej więcej mogę tak sobie to wybrażać? obszar (zbiór) otwarty i wewnątrz krzywa jordana a w niej punkt z0? no i jak już mam te z0 np 2i to jak wyliczyć całkę z tego? Bo chyba nie tak jak normalną zwykłą całkę dla liczb rzeczywistych.

ICSP: Jak masz z₀ to podstawiasz do wzoru:

	f(z)
∫γ		dz = 2πif(z0)
	z − z0

u ciebie z₀ = 2i

1		ez
	musisz na siłę wypchnąć do licznika i dlatego twoje f(z) =
z		z

Rysunek ok.

Lukasz: aaa dobra już mniej więcej kumam

	dz
a np z ∮		to z tego wypycham f(z) żeby zgadzało się do wzoru z−z0
	(z2+9)2

	dz		1
czyli będzie ∮		−> f(z) =		z0=3i
	(z−3i)(z−3i)(z+3i)2		(z−3i)(z+3i)2

ICSP: z₀ = 3i

	dz		1   (z + 3i)2
∫		= ∫		dz
	(z−3i)2(z+3i)2		(z − 3i)2

i korzystasz z uogólnionego wzoru:

	f(z)		2πi
∫		dz =		f(n)(z0)
	(z − z0)n+1		n!

u ciebie n = 1 oraz f⁽ⁿ⁾(z₀) oznacza n−ta pochodną funkcji f(z)

Lukasz: Dobra dzięki wielkie ! jak coś to będę tu pisał jeszcze w sprawie pytań to może przy okkazji zobaczysz . Dzięki

Lukasz: A w sumie, bo teraz siedzę nad tymi zadaniami, to jak obliczyć pochodną z funkcji f(z) =

	1
	(z+3i)2

piotr: stosując wzór (zⁿ)' = nzⁿ⁻¹ czyli ((z−3i)⁻²)' = −2(z−3i)⁻³

Lukasz: @Piotr czyli tak samo jak normalną funkcję? I czy tam nie powinno być −2(z+3i)⁻³?