Dowód ze stycznymi do okręgu
Bart: Wykaż, że styczne do okręgu x
2 +y
2 −8x+4y +15=0 poprowadzone przez punkt A = (3,1)
są prostopadłe.
Czy jeśli napisze równanie okręgu w punkcie A o takim samym promieniu co okrąg z równania
x
2 +y
2 −8x+4y +15=0 czyli
√5 i przyrównam 2 równania do siebie żeby dostać punkty
styczności
i następnie obliczę pod jakim kątem się przecinają to będzie to zaliczone na maturze (zdanie
wzięte
ze strony
https://zadania.info/d1/2962121 gdzie nie ma takiego rozwiązania, a wydaje mi się być
najłatwiejsze) ?
21 sty 15:58
21 sty 16:01
jc: Tak będzie ⇔promień okręgu * √2 = odległość środka okręgu od punktu A
x2+y2−8x+4y+15=0
(x−4)2 + (y+2) = 5
(4−3)2 + (−2−1)2=10
Faktycznie 5*2=10, czyli styczne są do siebie prostopadłe.
21 sty 16:07
Bart: Dokładnie też tak to obliczyłem, ale wolałem się dopytać czy na maturze przy opisaniu
wszystkeigobyłby max

21 sty 16:08
jc: Nie wiem, jak takie rozwiązanie byłoby ocenione.
21 sty 16:57
ABC:
jak to mówią w takich przypadkach " proszę udowodnić że pańska metoda daje dobry wynik" więc
zawczasu zalecam potrenować odpowiedni opis przy używaniu niestandardowych metod
21 sty 17:02
VII:
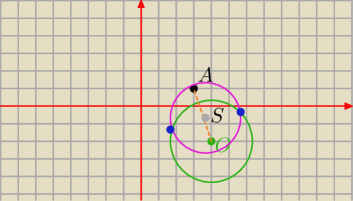
S=(4,−2)
A=(3,1)
Licze dlugosc odcinka AO
|AO|=
√(4−3)2+(−2−1)2=
√10
| | √10 | |
Promien nowego okregu to r= |
| |
| | 2 | |
Licze wspolrzedne srodka odcinka AO
Teraz ze srodka odcinka A0 promieniem AS rysuje okrag ktory przecina tamten okrag w dwoch
punktach
Tak wyglada konstrucja z geometrii elementarnej
Rownanie nowego okregu jest takie
| | 7 | | 1 | | √10 | |
(x− |
| )2+(y+ |
| 2=( |
| )2 |
| | 2 | | 2 | | 2 | |
| | 7 | | 1 | | 1 | |
(x− |
| )2+(y+ |
| )2= 2 |
| |
| | 2 | | 2 | | 2 | |
Wiec tez bedzie zabawa z liczeniem punktow stycznosci
21 sty 17:32
a@b:
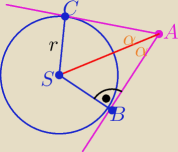
A(3,1) S(4,−2) r=
√5
|SA|=
√10
| | √5 | | √2 | |
W ΔABS : sinα= |
| = |
| |
| | √10 | | 2 | |
to α=45
o
2α=90
o
wniosek : styczne są prostopadłe
i po ptokach

21 sty 20:10

 S=(4,−2)
A=(3,1)
Licze dlugosc odcinka AO
|AO|=√(4−3)2+(−2−1)2= √10
S=(4,−2)
A=(3,1)
Licze dlugosc odcinka AO
|AO|=√(4−3)2+(−2−1)2= √10
 A(3,1) S(4,−2) r=√5
|SA|=√10
A(3,1) S(4,−2) r=√5
|SA|=√10
