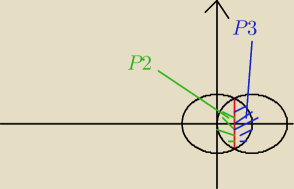
pole obszaru ograniczonego krzywymi x^{2}+y^{2}=1 i x^{2}+y^{2}-2x=0 Lukasz: Oblicz pole obszaru płaskiego ograniczonego krzywymi o równaniach x²+y²=1 i x²+y²−2x=0 Hej, potrzebuję pomocy, w zasadzie żeby ktoś mi to wytłumaczył. Zrobiłem sobie rysunek, widzę jakie pole musimy policzyć, te krzywe to 2 okręgi, 1 o środku (0,0) drugi o środku (1,0)

	−√3		√3
Oba mają punkt wspólny dla x=1/2 i y=		V y=
	2		2

No i myślałem żeby ten obszar policzyć poprzez podzielenie go na 2 pola. I ogólnie problem największy teraz to jakie ograniczenia tu dać? bo na postać biegunową jako tako wiem jak przejść ale jak zamienić ograniczenia x i y to tak średnio.

	√3		√3
moim zdaniem ogarniczenia dla pola 1 powinny być D:{ 1/2 ≤ x ≤ 1, −		≤y≤
	2		2

	√3		√3
a dla pola 2 { 0 ≤ x ≤ 1/2, −		≤y≤
	2		2

(widać na rysunku)

Qulka: podziel jeszcze na pół i policz całkę

Lukasz: Dobra, to jak podziele na jeszcze 2, to mam wtedy obszary Dla P1 D:{0≤φ≤π/3 , 1/2≤r≤1 i dla P2 D: {π/3≤φ≤π/2 , 0≤r≤2cosφ Bo policzenie całki to tam pikuś, ale właśnie chcę zrozumieć te przedziały.

Maciess: Czemu PI/3? Musisz tutaj użyć całek? Bo ten obszar mozna prosciej taką geometria szkolna policzyc

Maciess:

	1
A faktycznie PI/3 pardon. Pole mi wyszło		(8π−11√3)
	12

Lukasz:

	2		√3
@Maciess to źle ci wyszło, bo w odpowiedzi jest		π−
	3		2

Lukasz: Ponadto, tak jak pisałem chciałbym zrozumieć jakie tu mają być przedziały bo w rozwiazaniu np jest tak jak napisałem przedziały tylko w P1: 0≤r≤1

Maciess: W sensie ja nie za bardzo rozumiem o co właściwie pytasz. Może sprecyzuj to postaram sie pomoc.

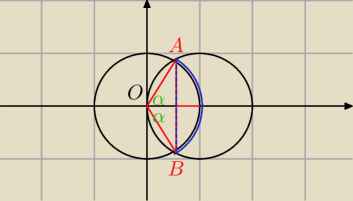
Saizou : x² + y² = 1 → S=(0; 0) r = 1 x² + y² − 2x = 0 → S=(0; 1) r =1 ================− 2x = 1

	1
x =
	2

	1		3
y2 =1−		=
	4		4

	1		√3
A=(		;		)
	2		2

	√3
sinα =		→ α = 60
	2

	120		1
P(wycinka) =		*π*12 =		π
	360		3

	1		√3		1		√3
P(ABO) = 2 *		*		*		=
	2		2		2		4

	1		√3
P(niebieskie) =		π −
	3		4

	1		√3		2		√3
P(obszaru) = 2(		π −		) =		π −
	3		4		3		2

Saizou : Za pomocą całki będzie P = 4* ∫_1/2¹ √1−x² dx = |podstawiamy x = sint → dx = cosx dx | = dokończ...

Lukasz: Dobra to sprecyzuję: zawsze przy liczeniu pól/objętości figur w przestrzeni wyznaczamy ograniczenia D dla x i y czyli np że x∊<0,1> y∊ < f(x), g(x) > ale w tym powyższym przykładzie nie wiem jakie dać przedziały.

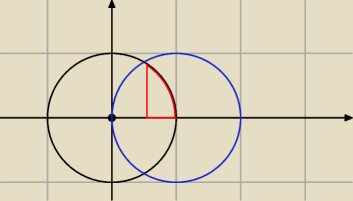
Qulka: 1 4•∫√1−x²dx 1/2

Lukasz: hmm, no tak wszystkie 4 części są takie same. ale gdyby np jedno z nich było większe to już nie można byłoby dać takiego czegoś. I na każdą część trzebaby dać inne ograniczenia.

Qulka: to wtedy składasz z kawałków i piszesz sumę całek zamiast 4•

Qulka: a i tak robisz cięcie na osi x bo całka to co pod osią X liczy na minusie

Lukasz: No dobra, to mniej więcej tyle rozumiem, ale właśnie ciągle chodzi o to żeby wiedzieć jakie przedziały dać do danego przykładu. No bo zobacz, ty sobie poszłaś od 1/2 do 1 i to jest 1 całka. Ale prawie zawsze używa się dwóch. Jedna określa się po dx a druga po dy. I np jak mam

	√3
przedział 0≤x≤1 0≤y≤		biorąc pod uwagę że koło nie jest na środku układu
	2

współrzędnych. to teraz jak zamienić ten zakres x i y na zakres r i φ

Qulka: niebieski łuk 1/2 y ∫ ∫ 1 dydx 0 0 i w miejsce y (górna granica) wstawiasz √1−x²+1 (tylko tu za ciasno i żebyś widział)