Okrag Khazix66: Wyznacz równanie okręgu, który jest styczny do prostych x=0 oraz 4x+3y+33=0, a także przechodzi przez punkt P=(−2,0), proszę o pomoc

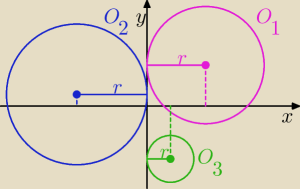
chichi: Wniosek? Dalej już powinno pójść, wzór na odległość punktu od prostej oraz odległość między punktami

Jerzy: Przecież żaden z tych okręgów nie przechodzi przez punkt P = (−2,0)

chichi: Ojj, @Jerzy... co ty nie powiesz. Wszystkie te okręgi są styczne do prostej o równaniu x=0 gdybyś nie zauważył, z tego rysunku wyciągnąć wniosek i zrobić następnie to co napisałem...

Khazix66: Czy chodzi o to że r=a?

chichi: Specjalnie narysowałem ten niebieski okrąg, abyś coś zauważył, a więc jeśli miałoby być r=a, a dla niebieskiego okręgu a<0 ⇒ r<0 sprzeczne Może wypadałoby zaatakować to modułem?

Khazix66: Próbuje cały czas i nie mogę dojść do rozwiązania, czy mogę prosić żeby ktoś rozwiązał?

Mila: Dobrze przepisane zadanie? Z jakiej książki?

chichi: A co jest nie halo @Mila?

Khazix66: Mila to zadanie z operonu i sprawdzałem na pewno dobrze przepisałem

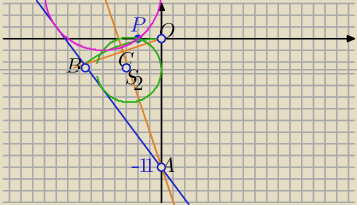
Mila: 4x+3y+33=0 A=(0,−11)

	4
y=−		x−11
	3

1) S=(p,q) − środek okręgu stycznego do ramion kąta leży na dwusiecznej tego kąta B(b₁,b₂)− punkt przecięcia prostej k i okręgu ośrodku A i R=11 b₁<0 x²+(y+11)²=11² i 4x+3y+33=0

	33		11
b1=−		, y=−
	5		5

	33		11
B=(−		, −		)
	5		5

2) ΔBOA− Δrównoramienny d: dwusieczna kąta BAO przechodzi przez środek BO i punkt A

	−33		11
C=(		,−
	10		10

d: y=ax−11 −(11/10)=a*(−33/10)−11 a=−3 y=−3x−11 3) r=|p| P=(−2,0)∊ okręgu (−2−p)²+(0+3p+11)²=p²

	25
p=−5 lub p=−
	9

	25		8
q=−3*(−5)−11=4 lub q=−		*(−3)−11=−
	9		3

S₁=(−5,4) r=5 lub

	25		8
S2=(−		,−		)
	9		3

Równania okręgów:

	25		8		25
(x+		)2+(y+		)2=(		)2
	9		3		9

(x+5)²+(y−4)²=25 ================

chichi: S=(a,b), r=|a|

	|4a+3b+33|		a−33
r=		⇒ 5|a|=|4a+3b+33| ⇒ b=		∨ b=−3a−11
	5		3

|a|=√(a+2)²+b² / ² ⇒ a²=(a+2)²+b² (1) Dla b=−3a−11

	25
a2=(a+2)2+(−3a−11)2 ⇒ 9a2+70a+125=0 ⇒ (9a+25)(a+5)=0 ⇒ a=−5 ∨ a=−
	9

	a−33
(2) Dla b=
	3

	a−33
a2=(a+2)2+(		)2 ⇒ a2−30a+1125=0 (Δ<0 ⇒ brak rozwiązań)
	3

Dla a=−5: r=|−5|=5 ∧ b=4, zatem: O₁: (x+5)²+(y−4)²=25

	25
Dla a=−
	9

	25		25		8
r=|−		|=		∧ b=		, zatem:
	9		9		3

	25		8		25
O2: (x+		)2+(y+		)2=
	9		3		9

chichi:

	25		8		25
O2: (x+		)2+(y+		)2=(		)2 oczywiście
	9		3		9

a@b:

Khazix66: Dziękuję za rozwiązania, a czy mógłby ktoś jeszcze pomoc mi z jednym dowodem geometrycznym z tego samego arkusza?

a@b: Mamy zgadywać treść zadania ?

Khazix66: A@b najpierw chciałem zapytać czy ktoś pomoże o co ci chodzi

Khazix66: Dany jest trapez prostokątny o podstawach a, b oraz wysokości długości 2h. Dłuższe ramię trapezu jest równocześnie średnica okręgu, który jest styczny do drugiego ramienia trapezu. Udowodnij, że h²=ab.

VII: Khazix66 U mnie mowi się tak Zapytać się możesz, ale wiesz co Cię to obchodzi

chichi:

	a+b
r=		⇒ 2r=a+b
	2

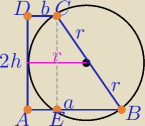
Z ΔCEB: |EB|=a−b (2h)²+(a−b)²=(2r)²=(a+b)² 4h²+a²−2ab+b²=a²+2ab+b² ⇒ 4h²=4ab ⇒ h²=ab Q.E.D.

VII: Widze że skorzystałes z twierdzenia o linii środkowej trapezu . Także mnie sie przyda .

chichi: Cześć @VII. Myślę, że to jest tak oczywiste, że nawet tego nie zapisywałem

VII: OK

Khazix66: Dziękuję chichi niby takie oczywiste a ja tego nie zauważyłem i nie mogłem przez to dojść do rozwiązania haha

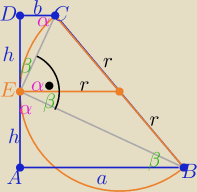
a@b: Z podobieństwa trójkątów ABE i DCE z cechy(kkk)

h		b
	=
a		h

h²=ab ====== i po ptokach

Szkolniak: Tak z ciekawości − miałby ktoś może odpowiedzi do matury próbnej z Operonu z poziomu rozszerzonego? Chętnie bym sobie sprawdził ile udało mi się zdobyć.

a@b: Jakiej matury, z którego roku ?

Szkolniak: Z tego. Mam ten arkusz, ale niestety nie jest nawet opisany rokiem i ciężko mi skonkretyzować który to jest, ale właśnie to zadanie się tam znalazło

chichi: No to do dwóch zadań już masz rozwiązania, wstaw resztę wyników bez rozwiązań, to sprawdzę później, bo mam arkusz gdzieś na kompie, ale szczerze to jeszcze go nie otwierałem, odkąd go mam, także pora go zrobić, jak już 2 zadania za mną

Szkolniak: Wstyd udostępniać, jeszcze wyjdzie że 20% mam Najbardziej w sumie interesuje mnie 13 zadanie, byłaby możliwość konsultacji teraz odnośnie niego? Bo ja jakoś dziwnie to zrobiłem i coś mi tu chyba nie pasuje

a@b: Napisz treść tego zadania

Szkolniak: Ciąg (a_n) jest ciągiem arytmetycznym. W wyniku podzielenia wyrazu a₁₃ przez a₃ otrzymujemy iloraz 5 i resztę 1, dodatkowo wyrazy pierwszy, siódmy, i sto trzeci w podanej kolejności tworzą ciąg geometryczny. Oblicz iloraz tego ciągu geometrycznego. Chętnie zamieszczę swoje rozwiązanie i tok rozumowania, bo strasznie jestem ciekaw czy jest dobrze, ale obstawiam że będzie kicha..

chichi: @Szkolniak wstyd to kraść... To zadanie jest tak banalne, że chyba ma z 3pkt. xD

Szkolniak: 4 ma − czy odpowiedź to 16?

chichi:

	5
Dla a1=1, r=		mamy:
	2

b₁=a₁=1 b₂=a₁+6r=1+15=16 b₃=a₁+102r=1+255=256

b3		b2
	=		=16
b2		b1

Dlaczego nie sprawdziłeś?

Mila: chichi, zniechęcasz takimi komentarzami do korzystania z forum 21: 12

Szkolniak: Skąd wziąłeś te wartości dla a₁ i r? Ja w ogóle podszedłem do tego w ten sposób: Mamy informację, że wyrazy a₁, a₇ i a₁₀₃ w podanej kolejności tworzą ciąg geometryczny, stąd: (a₇)²=a₁*a₁₀₃, gdzie a₇=a₁+6r i a₁₀₃=a₁+102r (a₁+6r)²=a₁(a₁+102r) a₁²+12a₁r+36r²=a₁²+102a₁r 45a₁r−18r²=0 r(45a₁−18r)=0

	18
r=0 v a1=		r
	45

Teraz sprawdzamy ten warunek z podzielnością a₁₃ i a₃: 1^o r=0, wtedy:

	a13		a1+12r		a1
		=		=		=1 (odpada)
	a3		a1+2r		a1

	18
v2o a1=		r
	45

	a7
q=		=16
	a1

Ma to sens? Też w sumie nie wiem czy w drugim przypadku nie powinienem sprawdzić co się dzieje gdy podzielę a₁₃ przez a₃?

chichi: @Mila nie wiem jak Ty to rozumiesz, ale jeśli on napisał, że wstyd publikować wyniki, a ja napisałem, że wstyd do kraść, to oznaczało żeby nie wstydził się publikować rozwiązań nawet jeśli nie ma pewności czy są poprawne. Co do drugiej części, to moja indywidualna opinia nt. zadania, a to czy ktoś się z tym zgadza ty nie, jego sprawa. Nie rozumiem Cię..

chichi: zgadza czy* nie

Mila:

a13		1
	=5+		⇔
a3		a3

a13−1
	=5
a3

a1+12r−1
	=5
a1+2r

a₁+12r−1=5a₁+10r 4a₁=2r−1, a₁ lub r podstaw do (a₁+6r)²=a₁(a₁+102r)

chichi: Wyjaśnienia skąd wziąłem wartości dla a₁ i r znajdziesz w poście @Mila

Szkolniak: Rzeczywiście. Szczerze mówiąc miałem wtedy zaćmienie i kompletnie nie wpadłem jak zapisać tą równość z podzielnością. A odnośnie mojego rozwiązania − mógłbym liczyć na pełną punktację czy raczej by mi nie zaliczyli?

Mila: Równość z podzielnością przez analogię:

12		2
	=2+
5		5

Szkolniak: Racja, pewnie musiałbym sobie gdzieś na boku rozpisać przykład taki na liczbach i bym zauważył

	a13
Ja myślałem żeby rozpisać coś typu		=5x+1, ale ten iks by mi tam wadził
	a3

Mogę zamieścić jeszcze jedno zadanko? Bo to ze słabego działu u mnie i też jestem bardzo ciekaw czy dobrze je zrobiłem

Mila: 21:4=5+r.1

21		1
	=5+
4		4

Szkolniak: Treść: W trójkącie równobocznym ABC na boku AB zaznaczono punkt D w taki sposób, że

	|AD|		1
		=		. Wyznacz sinus kąta BCD.
	|DB|		3

I wynik wyszedł mi dosyć 'dziwny'

	3√57
Wyszło mi: sinα=
	38

Filip: Generalnie źle, tu wystarczy rozwiązać układ równań a₁₃=5a₃+1 a₇²=a₁a₁₀₃ Poprawne odpowiedzi to q=16 v q=1

Szkolniak: Filip wiedziałem że fajnie by to poszło z układu równań, niestety tak jak powiedziałem, przez to że nie wpadłem na pomysł jak zapisać te pierwsze równanie to lipa

chichi: Szkolniak Pokaż jak liczyłeś

Filip: A z tym trójkątem to nie namieszałeś? Mi wyszło |CD|=x√13, a tobie x√19

chichi: Cześć @Filip to dobrze Ci wyszło

Szkolniak: Jak to? Mamy równanie: a²=25x²−12x²*cos(60^o)

	1
a2=25x2−12x2*
	2

a²=25x²−6x² a²=19x² a=x√19?

Filip: a²=b²−c²−2abcosα

Filip: a²=b²+c²−2abcosα Teraz to ja zrobiłem błąd

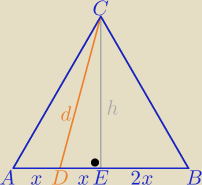
chichi: a=4x ⇒ h=2x√3 Z tw. Pitagorasa w ΔCED: (x)²+(2x√3)²=d² ⇒ 13x²=d² ⇒ √13x=d

Szkolniak: Szkoda, głupie błędy i punkty w plecy.. To jak już tak lecimy to możemy jeszcze sprawdzić ostatnie zadanie, czyli optymalizacyjne? Treść: Obwód trójkąta równoramiennego jest równy L. Jakie długości powinny mieć boki tego trójkąta, aby objętość bryły powstałej w wyniku obrotu wzdłuż podstawy była największa?

	3		3		L
Wyszło mi, że boki równe są		L,		L oraz
	8		8		4

Szkolniak:

	3√39
Teraz wychodzi tak: sinα=
	26

Filip: No generalnie według mnie boki ci wyszły poprawnie

chichi: @Szkolniak teraz jest okej

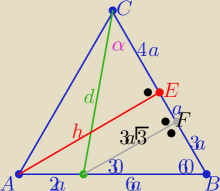
a@b: d²=25a²+27a² d=2√13

	3a√3
sinα=		=.........
	2√13

Filip: Cześć chichi Ad. 22:35

Szkolniak: 11 też było całkiem ciekawe, końcowo otrzymywało się równanie trygonometryczne dwukwadratowe, pierwszy raz się w ogóle z takim spotkałem, ale sprawdziłem na GeoGebrze i dobrze je rozwiązałem. 12 tez jest ciekawe − zamieszczę treść i jeśli ktoś miałby ochotę to chętnie sprawdzę czy dobrze zrobiłem.

	4−m
Treść: Dla jakich wartości parametru m funkcje f(x)=		oraz g(x)=x2+5x+m, dla x≠0, mają
	x

dokładnie trzy punkty wspólne? Mi wyszło, że m∊(−inf;7)∪(7;8)

Filip: W(x)=x³+5x²+mx−4+m=0 W(−1)=−1+5−m−4+m=0 W(x)=(x+1)(x²+4x+m−4) x²+4x+m−4 (1) Δ>0 Δ=16−4m+16>0 m<8 (2)x=√8−m−2!=−1 m!=7

chichi: @Szkolniak a jakie masz warunki?

Filip: A jakie to było 11 zadanie, bo nie mam wglądu?

Szkolniak: Filip

	3
11) Rozwiąz równanie sin2(2x)+1=7cos2(		π−x) dla x∊<−2π;2π>
	2

I co oznacza ten wykrzyknik przy m? chichi Δ>0 i f(−1)≠, gdzie f(x)=x²+4x+m−4

Szkolniak: f(−1)≠0, zero mi uciekło

Filip: No i jest ciekawy jakiś sposób by rozwiązać to zadanie, czy "na piechotę"?

a@b: Równanie:

	7
1−cos2(2x)+1=		*2sin2x , 2sin2x=1−cos(2x)
	2

i lecimy: 2cos²(2x)−7cos(2x)+3=0 (2cos(2x)−1)(cos(2x)−3)=0

	1
cos(2x)=		v cos(2x)=3 −− sprzeczność
	2

	π		π
2x=		+2kπ v 2x= −		+2kπ
	3		3

	π		5
x=		+kπ v x=		π+kπ , k∊C
	6		6

dla x∊<−2π, 2π> ........................... i po ptokach