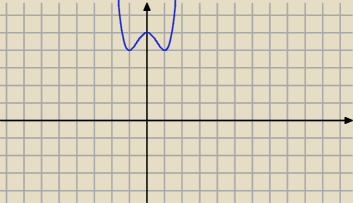
Znajdź najmniejsze i największe wartości funkcji: hamilton: Znajdź najmniejsze i największe wartości funkcji: f(x) = x⁴ − 2x² + 5, na przedziale [0; 2]

Jerzy:

hamilton: Hmmm a Pokazał by mi Pan rachunki algebraiczne by o wyliczyć?

Jerzy: Policz pochodną.

piotr: f(x) = x⁴−2x²+5 = (x²−1)² + 4 Czyli f(x) osiąga ekstrema w tych samych punktach co funkcja: |x²−1|

hamilton: @Jerzy wyliczyłem pochodną i co teraz?

Jerzy: f'(x) = 4x³ − 4x = 4x(x² − 1) i szukamy miejsc zerowych pochodnej.

hamilton: −1,0,1 f'(x) > 0 dla x (−1;0) u (1,+niesk) f'(x) < 0 dla (−niesk;−1) u (0,1)

hamilton: Mógłby Mi Pan napisać przepis co robić?

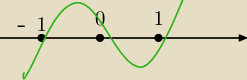
Jerzy: W punkcie x = 0 pochodna zmienia znak z dodatniego na ujemny, czyli funkcja z rosnącej przechodzi w malejąca, czyli ma maksimum lokalne. W punkcie x = 1 pochodna zmienia znak z ujemnego na dodatni,czyli funkcja z malejącej przechodzi w rosnącą, a więc ma tam minimum lokalne.

Jerzy: No i oczywiście policz f(0) m maksimum lokalne oraz f(1) (minimum lokalne )

Saizou : f(x) = x⁴ − 2x² + 5 = (x²−1)²+4 f_min(1) = 4 f_max(2) = 13