ekstrema funkcji uwikłanej Lukasz: Rozwiązanie mojego zadania na studia, na punkty, wstawiam tu bo muszę zrobić zdjęcie całego równania. y²−x³+2x²−x=0 fx=−3x²+4x−1 (pochodna względem x) 1^o y²−x³+2x²−x=0 −3x²+4x−1=0 z drugiego równania wyznaczam x: Δ=4

	1
x1=1 x2=
	3

Podstawiam do pierwszego równania: dla x=1: y²−1+2−1=0 y²=0 ⇔ y=0 P(1,0) ← punkt podejrzany o ekstremum

	1
dla x=
	3

y²+U{−1+6−9}=0

	4		−2√3		2√3
y2=		⇔ y=		v y=
	27		9		9

2^o

	1		−2√3		1		2√3
sprawdzamy ekstrema w punktach P1(1,0), P2(		,		), P3(		,		)
	3		9		3		9

	−fxx
y''=
	fy

fxx=−6x+4 fy=2y −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− Dla P1(1,0):

	−6+4
y''=−
	0

Ekstremum nie istnieje −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

	1		4√3
Dla P2(		,−		)
	3		9

	−2+4		2		3√3
y''=−		=		=		> 0 więc jest minimum
	4√3   −   9		4√3   9		2

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

	1		4√3
Dla P3(		,		)
	3		9

	−2+4		2		3√3
y''=−		= −		=−		< 0 więc jest maksimum
	4√3   9		4√3   9		2

	1		2√3
Odpowiedź: W punkcie (		,−		) jest minimum funkcji, a w punkcie
	3		9

	1		2√3
(		,		) maksimum funkcji
	3		9

jc: W punkcie (1,0) linie się przecinają i nie wiadomo jak określić funkcję, więc pytanie pytanie o ekstremum chyba nie ma sensu.

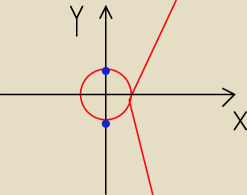Lukasz: @jc hmm linie się przecinają ale czy to ma znaczenie? rysunek mniej więcej. To te 2 punkty osiągają minimum i maksimum lokalne. Punkt przecięcia nie jest ekstremum więc tam go nie ma. Chyba że źle myślę (dopiero zacząłem ten temat studiować, samodzielnie bo nie mam jeszcze tego na wykładach)

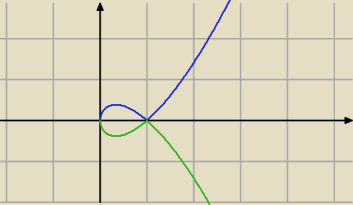Qulka: tak mniej więcej trochę przesuniętą miałeś jeśli chcesz funkcję to trzeba by ją rozbić na składowe bo inaczej to tylko krzywa ;>

Lukasz: @Qulka w sensie y²−x³+2x²−x=0 to jest krzywa? i jak rozbić na składowe

Qulka: definicja funkcji to: dla każdego x jest tylko 1 y więc tu nie pasuje... składowa niebieska i zielona