. Jan: Napisz równanie prostej k przechodzącej przez punkt m i prostopadłych do prostych l1,l2 M=(1,1,0) l1 x=2t+1 y=4t−1 z=t l2= 2x−y+z−1=0 x+z=0 Ja to zrobiłem w ten sposób, wektor l1(2,4,1) pomnożyłem wektorowo przez wektor l2 (−1,−1,1) Wektor prostej k to (5,−3,2) k= x=5t+1 y=−3t+1 z=2t Pytanie moje brzmi następująco, skoro pr. k jest prostopadła do l1 i l2, to l1 i l2 powinny być do siebie równoległe, czyli ich wektory powinny być takie same, a nie są.

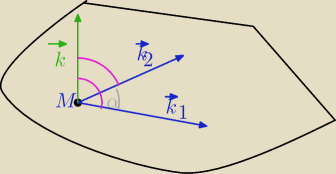
Mila: 1) k₁^→=[2,4,1]−wektor kierunkowy prostej l₁ 2) prosta l2: 2x−y+z−1=0 x+z=0 Równanie parametryczne prostej l₂: y=t 2x+z=1+t x+z=0 ======= (−) x=1+t y=t z=−1−t k₂^→=[1,1,−1]− wektor kierunkowy prostej l₂ ========= 3) wektor prostopadły do k₁ i k₂ k^→=[2,4,1] x [1,1,−1]=[−5,3,−2] || [5,−3,2]− wektor kierunkowy prostej k Równanie prostej k, M=(1,1,0)∊

x−1		y−1		z
	=		=
5		−3		2

======================== k ⊥ k₁ i k ⊥ k₂ [5,−3,2] o [2,4,1]=10−12+2=0 [5,−3,2] o [1,1,−1]=5−3−2=0

Jan: Dziękuje Pani bardzo, rysunek pomógł bardzo.

Mila: Gdyby było l₁||l₂ , to trzeba inaczej rozwiązywać.