Kąt 'Kąt: "Dany jest kąt ostry α i punkt P leżący wewnątrz kąta na jego dwusiecznej i w odległości d od wierzchołka kąta. Najmniejszy obwód trójkąta o jednym wierzchołku w punkcie P , a pozostałych wierzchołkach po jednym na każdym z ramion kąta równy jest: " a)dtg α/2 (1+2cosα) b)dtg α/2 (1 + cosα) c)2dtg α/2 d)2dtg α/2 (1+cosα) Nie wiem jak to rozwiązać, dodam że poprawna może być więcej niż 1 odpowiedź.

Eta: Odp: D)

plisss: A jak to obliczyć?

Kuba: ?

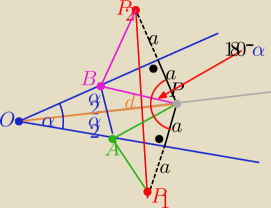
a@b: Obwód APB = długość łamanej P1ABP₂ Najmniejszy obwód ΔAPB = |P1P₂| Z tw. cosinusów w ΔPP1P2 |P1P2|²= 4a²+4a²+2*2a*2a*cosα , |∡P1PP2|=180^o−α

	a
|P1P2|2= 8a2(1+cosα) i		= sin(α/2) to a=d*sin(α/2) i 1+cosα= 2cos2(α/2)
	d

|P1P2|²= 16d²sin²(α/2)*cos²(α/2) = 4dsin²α |P1P2|=2dsinα =========== takiej odpowiedzi nie masz zatem

	cos(α/2)
|P1P2|= 2d*2sin(α/2)*cos(α/2) *
	cos(α/2)

|P1P2|= 2dtg(α/2)*2cos²(α/2) |P1P2|= 2dtg(α/2)(1+cosα) ===================

Mila:

a@b:

rafał hajdo:

a@b: Co mnie tak "prześladujesz"

rafał hajdo: Eta jest super

a@b: Łap .. i mnie nie osłabiaj

rafał hajdo: