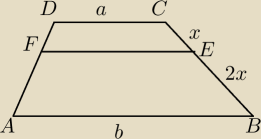
 Ramię BC trapezu zostało podzielone tak jak pokazano na rysunku.
Korzystając z informacji, że długość krótszej podstawy to a, oraz długość dłuższej podstawy b,
wyznacz długość odcinka EF, który jest równoległy do obu podstaw.
Czy zechce ktoś podpowiedzieć jakieś wskazówki do tego zadania?
Pierwsza myśl to twierdzenie Talesa, ale po kilku próbach nie otrzymałem nic ciekawego.
Czy EF to średnia harmoniczna podstaw trapezu?
Ramię BC trapezu zostało podzielone tak jak pokazano na rysunku.
Korzystając z informacji, że długość krótszej podstawy to a, oraz długość dłuższej podstawy b,
wyznacz długość odcinka EF, który jest równoległy do obu podstaw.
Czy zechce ktoś podpowiedzieć jakieś wskazówki do tego zadania?
Pierwsza myśl to twierdzenie Talesa, ale po kilku próbach nie otrzymałem nic ciekawego.
Czy EF to średnia harmoniczna podstaw trapezu?
| 2a+b | ||
|EF|= | ||
| 3 |
| y | y+x | y+3x | ||||
Wynika to z układu | = | = | ||||
| a | |EF| | b |


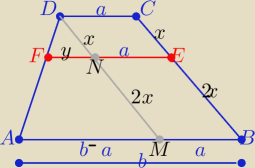 2 sposób
|EF|=a+y
i z podobieństwa trójkątów AMD i FND :
2 sposób
|EF|=a+y
i z podobieństwa trójkątów AMD i FND :
| b−a | b−a | |||
=3 ⇒ y= | ||||
| y | 3 |
| 2b+a | ||
to |EF|= | ||
| 3 |
| 2a+b | ||
oczywiście ma być: |EF|= | ||
| 3 |