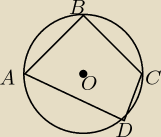
Geometria XZ: W okrąg o środku O i promieniu długości 4 wpisano czworokąt ABCD, w którym |AB| = |BC| oraz |∡ADC| = 120 stopni. Stosunek pola trójkąta ADB do pola DCB wynosi 3:1. Oblicz obwód i pole czworokąta ABCD

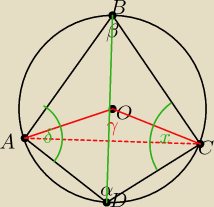
Basia: α=120 ⇒ β=60 ⇒ tr.ABC jest równoboczny β=60 ⇒ γ=120 z tw.cosinusów można policzyć AC=AB=BC=a a² = r²+r²−2r*r*cos120 a² = 16+16−2*4*4*(−¹₂) a² = 32+16 a²=48 a=4√3 x=180−δ

	a*AD*sinδ
PABD =
	2

	a*BC*sin(180−δ)		a*BC*sinδ
PBCD =		=
	2		2

stąd

a*AD*sinδ		3
	=
a*BC*sinδ		1

AD
	=3
BC

AD=3BC BC=b AD=3b znowu z tw.cosinusów a² = b²+(3b)²−2b*3b*cos120 a² = 10b²+6b²*¹₂ /*2 a²=10b²+3b² a²=13b² mając a wyliczysz b 48 = 13b²

	48
b2 =
	13

	4√3
b =
	√13

Ob = 2a+4b P = ¹₂a*a*sin60 + ¹₂b*3b*sin120

XZ: Dziękiii Wielkie

Szymon: a takie pytanie jeżeli na samej górze jest że: z tw.cosinusów można policzyć AC=AB=BC=a to dlaczego później jest że odcinek BC oznaczamy przez b dodatkowo skoro wiemy że ma taką samą wartość jak a mamy już go policzonego? chyba że czegoś tu nie rozumiem.

XZ: Nie po prostu koleżanka zamiast DC napisała BC.

Szymon: i wszystko jasne.

yolo: Mam pytanie, skoro AC=AB=BC=a, a β=60 i wynika z tego ze ABC to trojkat rownoboczny, to czemu nie mozna by obliczyc a ze wzoru na wysokosc trojkata wpisanego w okrag ? Wtedy a=6√2...

kris: oczywiście że można kolego, tylko że to i tak wychodzi 4*sqrt(3) bo 4 = 2/3 h ⇒ h = 6 w trójkącie równobocznym: h = (a*sqrt(3))/2 ⇒ a=4sqrt(3)

Wera: w polu P_BDC nie ma przypadkiem pomyłki, że zamiast BC ma być DC

pask550: Jest