Oblicz pole powierzchni płata wyciętego z powierzchni z=4-p{x^{2}+y^{2}} Lukasz: Oblicz pole powierzchni płata wyciętego z powierzchni z=4−√x²+y² powierzchnią x²+y²=4y Przedstaw na rysunku. Hej. Nie wiem po czym całkować obszar, nie wiem jak by to dalej ugryźć. powierzchnia z to stożek, a rownanie drugiej pow. przekształcam na równanie koła wychodzi x+(y−2)²=4 r=2 S(0,2) Nie wiem czemu ale nie jest on ograniczony żadną osią np z=0 zeby ten stozek nie leciał w −oo ale okej (mimo że w rozwiazaniu wydaje sie jakby bylo policzone tak jakby byl uciety, bo jak mozna obliczyc pole czegos co nie jest ograniczone) no ale okej ograniczyłem obszar D:{ 0≤r≤4cosφ , 0≤φ≤π i nie wiem co dalej, po czym całkować Ktoś jest w stanie mi podpowiedzieć? Pozdrawiam

Maciess: Generalnie to nie równanie koła (okręgu), bo rzecz dzieje się w przestrzeni więc jest walcem (pustym w środku tak jakby).I tenże walec jak foremka wycina z ciasta pewną część wykresu z. No ale interpretujemy to zadanie tak, że liczysz pole płata z funkcji z=f(x,y), w obszarze z dziedziny. W tym wypadku nad KOŁEM P={(x,y): x²+(y−2)²≤4} f(x,y)=4−√x²+y² Pole płata ∫∫_P √1+(f'_x)²+(f'_y)² dω No i pewnie trzeba na biegunowe przejść zeby łatwiej poszło. Rysunek z geogebry: https://www.geogebra.org/3d/edaummc8

Lukasz: @Maciness, dzięki za odpowiedź. Ogólnie to wiem że to jest walec, ale równaniem koła to to chyhba dalej się nazywa? (Nie ważne). Do momentu wyobrazenia tego doszedłem, rysunek mmam też identyczny jak twój z geogebry. Tylko właśnie czy to nie jest trochę źle napisane w zadaniu że nie jest ograniczony osią Z? bo ten walec też idzie do −oo czyli pole jest nieskończenie wielkie czy nie? Okej, co do dziedziny, to rozumiem że biorę równanie stożka i ograniczam go dziedziną walca? No i wtedy byłoby tak jak napisałeś f(x,y)=4−√x²+y² przechodzę na biegunowe wychodzi D: { 0≤r≤4cosφ , 0≤φ≤π } i liczę π 4cosφ ∫ { ∫ 4−√r²cos²φ+r²sin²φ dφ } dr 0 0 i nie wiem co to jest te twoje równanie na pole płata ∫∫p ... ? co to za pierwiastek ?

Lukasz: w sensie ten pierwiastek twój jest dobry tzn w rozwiazaniu jest tak samo napisane ale skąd to się wzięło

Maciess: Zadanie jest sformułowane raczej poprawnie. Przyjrzyj się rysunkowi jeszcze raz. Tak jakbys parasolke przebił okrągłym profiem stalowym. W środku proflu pozostanie materiał (ten o który chodzi w zadaniu). Reszta parasola w naszym przypadku jest dość kłopotliwa, bo nieograniczona i domyślamy się, że nie o nią chodzi. To co napisałeś to można zinterpretować jako objętość figury. Ty masz policzyć pole. koło ≠ okrąg i o taką kwestie techniczną mi chodziło. P to obszar po którym całkujemy. Pole powierzchni liczymy inaczej i to własnie wyraza ten tajemniczy zapis z brzydkim pierwiastkiem. Ide coś zjeść, potem moge to przeliczyć (o ile ktoś mnie nie uprzedzi) i pokaże cały tok rozumowania.

Maciess: A jak jestes ciekaw, skąd pierwiastek to musisz wziąc jakiś solidny podręcznik do analizy i poczytać

Lukasz: Dobra, teraz rozumiem haha ciągle źle do tego podchodziłem i ciągle chciałem objętość liczyć Ah ta parasolka. Do tego ciągle myślałem że jest osobny wzór na pole ... Dzięki wielkie Maciess, mega mi pomogłeś. A to skąd się wziął pierwiastek to odpowiedzią dla mnie wystarczającą jest: bo jest tak we wzorze . Pozdrawiam !

Lukasz: w sensie myślałem że nie ma osobnego wzoru na pole*

Lukasz: Jeszcze takie pytanie, bo wyliczyłem ten pierwiastek, wychodzi √2 π 4cosφ teraz daje ten pierwiastek przed całą całkę i jest: √2 ∫ dφ ∫ dr 0 0 no i normalnie zamieniam x=rcos y=rsin ale tu nie ma ani x ani y. I w rozwiazaniu po podstawieniu wychodzi całka ∫r dr i teraz pytanie, jak to sie bierze? (wiem że normalnie przy zamianie mnoży się też za jakobian ale tu to wychodziłoby 0*r)

Maciess: Czemu 0? A nie 1*r? Dodatkowo jak w biegunowych to raczej r sie zmienia przy ustalony kącie od 0 do 4sinφ Chociaz tu mozna by było raczej sobie dac rade bez ukladu biegunowego.

Maciess:

r
	=sinα ⇒ r=4sinα
4

f(x,y)=4−√x²+y² f'²_x+f'²_y=1 0<α<π 0<r<4sinα ∫∫_P √1+1 dω = √2 ∫∫r drdα = √2/2∫r² dα = 8√2∫sin²α=

	cos2α+1
=8√2 ∫ 1−cos2α dα=8√2(π−∫		dα =4√2(π−∫cos2α dα) = 4√2(π−0)=4√2π
	2

W przedostatnim przejsciu wykorzystalem fakt, ze całka z cos2x po pelnym okresie to 0. Powinno byc okej

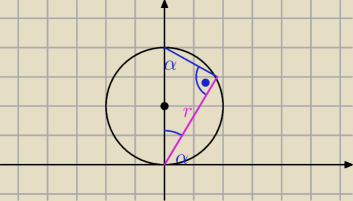
jc: Można bez całkowania. Po rozwinięciu stożka zobaczymy ściśnięte kątowo koło (dzielimy przez √2) o promieniu 2√2. Pole = [π (2√2)²]/√2=π4√2.