graf hamiltonowski
grafik: Jakie warunki musi spełniać graf Kn1n2n3, aby był hamiltonowski ( ma cykl Hamiltona)?
15 sty 19:48
kerajs: Jeśli ten dziwny zapis oznacza graf trójdzielny o licznościach wierzchołków n1, n2 i n3 to
warunkiem będzie:
2 max{n1,n2,n3}=n1+n2+n3
najliczniejszy nx jest sumą pozostałych
17 sty 09:45
grafik:
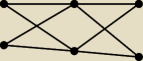
Dla takiego grafu mamy liczności:
n
1 = 2
n
2 = 4
n
3 = 2
Powyższy warunek jest spełniony, ale ja w nim nie widzę cyklu Hamiltona.
17 sty 11:19
kerajs: Zgadza się. W grafie K2,4 który narysowaleś/łaś nie ma cyklu Hamiltona.
17 sty 12:15
grafik: Aaa, teraz rozumiem. Żle rozumiałem definicję grafu trójdzielnego. Dziękuję bardzo!
17 sty 12:45
 Dla takiego grafu mamy liczności:
n1 = 2
n2 = 4
n3 = 2
Powyższy warunek jest spełniony, ale ja w nim nie widzę cyklu Hamiltona.
Dla takiego grafu mamy liczności:
n1 = 2
n2 = 4
n3 = 2
Powyższy warunek jest spełniony, ale ja w nim nie widzę cyklu Hamiltona.