trójkąt micho: Dany jest trójkąt ABC,w którym < BAC=60^o Na bokach AB i AC wybrano odpowiednio punkty P i Q tak,że PB=PQ=QC Oblicz miarę kąta BCP

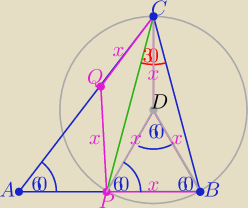
Eta: Rysunek................... 1/ wybieram punkt D tak, by czworokąt CQPD był równoległobokiem zatem po uwzględnieniu danych z treści zadania mamy ΔPBD równoboczny 2/ na ΔCPB można opisać okrąg o środku w punkcie D i promieniu "x"

	1
i mamy |∡BCP|=		|∡PDB| dlaczego? (odpowiedz sam ........
	2

Odp: |∡BPC|=30^o =============

janek191: ?

Eta: @Janek191 Co Ci nie pasuje ?

Eta: Aaaa chyba,że ..........ten chochlik |∡BCP|=30^o

chichi: Cześć @Eta fajne rozwiązanie, proste i przejrzyste

Eta: Hej chichi

VII: Tyle że na maturze nie pozwolom mi wziąć kolorowych pisaków

Eta: To sobie postawisz kreseczki na bokach równej długości

chichi: @VII tym się nie przejmuj, możesz nawet boki cieńszą, czy to grubszą linią narysować, to egzaminator będzie się głowił. Ważne, aby wierzchołki były poprawnie oznaczone, na rysunek nawet nie trzeba nanosić danych, ale robi się to po prostu dla twojej wygody jak i egzaminatora

VII: QCIIPD =x Kąt przy P=60^o odpowiadajacy przy A Skad wiemy ze kąt DBP= 60^o ?

VII: chichi Nie przejmuje sie

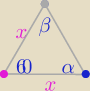
Eta: α=β=60^o

VII: Już rozumiem.