dowód mydlix: Udowodnij, że jeśli a² + b² ≤ 2, to a + b ≤ 2

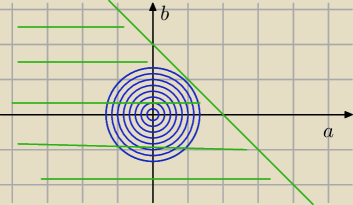
Qulka: każdy punkt niebieskiego koła leży poniżej zielonej prostej lub się styka bo odległość środka od prostej =r

mydlix: Dziękuję, ale czy ktoś umie to zrobić metodami algebraicznymi?

chichi: Jeżeli są założenia jakieś co do liczb, mianowicie a,b>0 to można z nierówności Cauchy'ego między średnimi

Qulka: ale Pani egzaminator w zeszłym miesiącu powiedziała że geometryczny do tego jest najlepszą metodą

Minato: Am ≤ Kw

a+b		a2+b2		2
	≤ √		≤ √		= 1
2		2		2

a+b ≤ 2

ICSP: a + b ≤ |a+b| = √(a+b)² ≤ √(a+b)² + (a−b)² = √2(a² + b²) ≤ √2*2 = 2

getin: ogólnie wiadomo, że (a−b)²≥0 (a−b)²≥0 a²−2a*b+b²≥0 a²+b²≥2a*b 2a*b≤a²+b² 2a*b≤a²+b²≤2 2a*b≤2 a²+b² ≤ 2 dodajemy stronami 2a*b a²+2a*b+b² ≤ 2 + 2a*b a²+2a*b+b² ≤ 2 + 2a*b ≤ 2 + 2 (a+b)² ≤ 2 + 2a*b ≤ 4 (a+b)² ≤ 4 przy założeniach a≥0, b≥0 otrzymujemy a+b ≤ 2 dla a,b różnych znaków i takich że a+b>0 mamy 2a*b < 0 a²+b² ≤ 2 dodajemy stronami 2a*b a²+2a*b+b² ≤ 2 + 2a*b a²+2a*b+b² ≤ 2 + 2a*b ≤ 2 + 0 (a+b)² ≤ 2 + 2a*b ≤ 2 (a+b)² ≤ 2 a+b ≤ √2 a jeśli coś jest mniejsze od √2 to automatycznie jest mniejsze od 2 dla a,b różnych znaków i takich że a+b<0 mamy od razu tezę jeśli a+b<0 to automatycznie a+b≤2 dla a,b ujemnych tzn. a+b<0 od razu mamy tezę

mydlix: Dziękuję bardzo

ICSP: Skoro 2ab ≤ 2 to (a+b)² ≤ 2 + 2ab ≤ 2 + 2*1 = 4