Geom Gabrysiaaa: Mam jeszcze takie jedno zadanie z którym nie mogę sobie poradzić.

	25		25		1
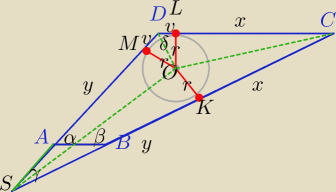
W wypukłym czworokacie ABCD: AB=		, BC=12		, CD=6		,kat DAB jest ostry, kat
	64		64		4

	3		63
ASC jest rozwarty, sin(DAB)=		, cos(ABC) =−		. Okrąg o środku w O jest styczny do
	5		65

boków BC, CD i AD. Oblicz OC.

Mila: kąt ASC ? Gdzie jest punkt S?

Gabrysiaaa: Mila tam jest ADC, przypadkiem źle kliknęłam na klawiaturze

chichi: Idzie się namęczyć, sprawdzałem poprawność obliczeń dwa razy i wynik wychodzi mi dość brzydki,

	√130
póki co stawiam, że |OC|=		, aczkolwiek poczekaj na opinie bardziej doświadczonych
	2

ekspertów czy w przypadku tego forum raczej ekspertek od geometrii

an: Wynik chichi wygląda na prawidłowy, z Geogebry wychodzi 5,7008771255 czyli to samo

chichi: To super, dzięki an, jak nikt nie wrzuci rozwiązania, to postaram się wieczorem przepisać

Mila:

	3		63
sinα=		, cosβ=−
	5		65

	25		25		1
|AB|=		, |BC|=12		, |DC|=6
	64		64		4

K,L,M punkty styczności okręgu do odpowiednich boków czworokąta i jednocześnie boków ΔSCD. 1) WΔSAB:

	3		63
sinA=		, cosB=
	5		65

	4		16
cosA=−		, sinB=
	5		65

sinγ=sin(180−(A+B))=sin(A+B)

	3		63		16		4
sin(A+B)=		*		+		*(−		)⇔
	5		65		65		5

	5		12
sinγ=		, cosγ=
	13		13

=============

AB		SB
	=		⇔|AB|*sinA=|SB|*sinγ⇔
sinγ		sinA

25		3		5
	*		=|SB|*
64		5		13

	39
|SB|=
	64

	39		25
|SC|=		+12		⇔
	64		64

|SC|=13 2) W ΔDCS:

13		DC		5		25
	=		⇔13*		=		*sinδ
sinδ		sinγ		13		4

	4		3
sinδ=		, cosδ=−		( kąt rozwarty)
	5		5

3)

	γ		sinγ		5   13
ctg		=		=		=5
	2		1−cosγ		12   1−   13

W SOK:

	γ		y		y
ctg		=		,		=5⇔y=5r
	2		r		r

	δ		sinδ		4   5		1
ctg		=		=		=
	2		1−cosδ		3   1+   5		2

	1		v
W ΔDOL:		=		⇔
	2		r

	1
v=		r
	2

======== 4)

	1
v+x=6		, y+x=13
	4

	1		1
x+		r=6
	2		4

x+5r=13 −−−−−−−−−−−

	11		3
x=		, r=
	2		2

5) FINAŁ

	121		9
|OC|2=		+
	4		4

	√130
|OC|=
	2

================