Ekstrema funkcji misiaczek: dzień dobry , czy mógłby mi ktoś pomóc wyznaczyć ektrema i monotoniczność funkcji f(x)=x*e^1/x wychodzi mi pochodna: (e^1/x*x−e^1/x)/x i po przyrównaniu jej do zera dostaje ekstremum równe 1 ,ale po sprawdzeniu przedziały monotoniczności nie zgadzają się z wykresem funkcji

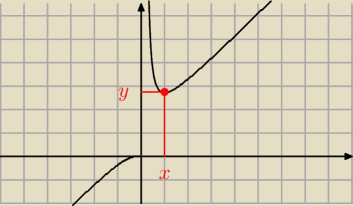
Minato: Funkcja y jest określona dla x∊R\{0} y = x*e^1/x

	1
ln y = ln(x*e1/x)= lnx + lne1/x = lnx +
	x

1		dy		1		1
	*		=		−
y		dx		x		x2

dy		1		1		1		1		1
	= (		−		)*y = (		−		)*x*e1/x = (1−		)e1/x
dx		x		x2		x		x2		x

	1
(1−		)e1/x = 0
	x

	1
1−		= 0 lub e1/x = 0 (sprzeczne)
	x

x₀ = 1 Monotoniczność

	1
(1−		)e1/x > 0
	x

	1
1−		> 0
	x

(x−1)x>0 (−∞; 0) oraz (1:+∞) (dla takich x−ów funkcja y rośnie) (0, 1) (dla takich x−ów funkcja y maleje), zatem w x₀ = 1 mamy ekstremum lokalne.

misiaczek: nie wiem czemu ale na wolframie dostaje inną pochodną

misiaczek: dobra , jednak sie zgadza mój błąd