Geom Gabrysiaaa: Dany jest wycinek koła o kącie wypukłym równym α oraz promieniu r. W wycinek ten wpisano prostokąt w ten sposób, że dwa wierzchołki prostokąta leżą na łuku wycinka zaś dwa pozostałe na promieniach ograniczających ten wycinek. Obliczyć pole tego prostokąta oraz zbadać, kiedy to pole osiąga wartość największą. Czy mogłabym prosić o jakieś nakierowanie? Próbowałam parę razy i poza rysunkiem i paroma linijkami nie jestem w stanie dojść do wyniku. Albo jakie twierdzenie muszę wykorzystać w tym zadaniu.

Mila:

	α
β=		, 0<α<π
	2

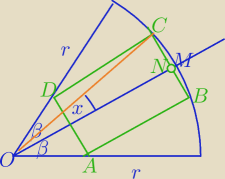
OM− dwusieczna kąta α ∡COM=x 1) W ΔCON:

	|CN|
sinγ=		⇔|CN|=r*sinx
	R

	ON
cosγ=		⇔|ON|=r* cos x
	R

|KN|=|ON|−|OK| 2) w ΔOKA:

	OK|
ctgβ=		, |AK|=UCN|
	|AK|

	α
|OK|=ctg		*r sinx
	2

	α
|KN|=r*cosx−ctg		*r sinx
	2

3) Pole prostokąta :

	α
S(x)=(r cosx−ctg		*r sinx)*2*r*sinx
	2

	α
S(x)=2r2 sinx*(cosx−ctg		*sinx)
	2

3) Licz teraz S'(x) Możesz przekształcić wcześniej wzór S(x), ale możesz podanego też pochodną policzyć, wolfram pomoże.

	α
wynik x=
	4

chichi: Ja robiłem przekształceniami, doszedłem do wyniku, ale gdybym miał te obliczenia przepisać na forum to bym do 22 siedział

	α
Tak czy inaczej Pmax dla θ=		, przy czym u mnie 'θ' to 'x' u @Mila
	4

	r2		α		α
P=		(cos(2θ−		)−cos(		))
	α   sin   2		2		2

Taki wzór otrzymałem pomijając pochodną A ty @Mila pochodną czy wrąbałaś się w przekształcenia jak ja?

Mila: chichi Za mnie pochodną policzył wolfram z podanego wzoru.. Przecież nie mogę całego rozwiązania wpisać, bo zostanę wyklęta za demoralizację młodzieży, jak to już bywało.

chichi: Ciekawi mnie czy takie pochodne dziś są w programie szkoły średniej, no chyba, że zadanie nie pochodzi z tego poziomu To by wszystko wyjaśniało dlaczego trzeba się tyle napracować

Mila: Może jutro przeliczę. Zobaczymy , czy Gabrysia napisze z jakiego jest poziomu edukacji. Chichi, ciekawa jestem w jaki sposób ustaliłeś kąty w zadaniu Rumcajsa. Czy odgadłeś coś, czy uzasadniłeś?

chichi: @Mila oczywiście, że uzasadniłem, w jaki sposób mogłem odgadnąć? za mała szansa żeby trafić

Gabrysiaaa: Dziękuję

Gabrysiaaa: Dodałam również inne zadanie z którym też nie mogę sobie dać rady