Wektory mature29: Dane dwa wektory A, B, są 2−ma przekątnymi sąsiednich sobie ścian sześcianu, które pochodzą z jednego wierzchołka. Przyjmij że długość boku to 'a'. Oblicz iloczyn skalarny wektorów oraz iloczyn wektorowy (obydwu przypadków AxB i BxA)

mature29: próbuję od godziny złapać nawet początek, ale coś nie idzie proszę o pomoc

kerajs: Na początek: kąt między tymi wektorami to 60 stopni.

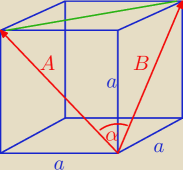
janek191: α = 60^o I A I = a√2 I B I = a √2 Mamy Iloczyn skalarny

	1
A o B = I AI*I B I * cos α = 2 a2*		= a2
	2

Iloczyn wektorowy

	√3
I A x B I = I A I* IB I*sin α = 2 a2*		= √3a2 − długość A x B
	2

mature29: czy ten kąt mówi nam coś więcej niż informacja że przekątne mają długość a√2 ? nawet jeżeli, to nie potrafię sobie wyobrazić obliczeń wymaganych iloczynów. zakładając że wektory są sobie przeciwne, to iloczyn skalarny chcąc nie chcąc, wychodzi −2a² ale czy to dobra analiza? w jaki sposób poradzić sobie z iloczynem wektorowym?

mature29: ups − nie odswiezylem strony od godziny 12−ej teraz widzę i dziękuję