Dla jakich wartości parametru m rozwiązaniem układu równań jest para liczb x y qTarantin0: Dla jakich wartości parametru m rozwiązaniem układu równań jest para liczb (x,y) spełniająca nierówność x+y ≥ 1? my−9x=−4 mx−y=m wyliczyłem x= m²−4 / m²−9 y = m(m²−4 / m²−9)−m Po zrobieniu nierówności wyszło mi, że m≥−1, a w odpowiedzi jest m∊(−3,−1> ∪ (3,+∞), wie ktoś może dlaczego tak jest?

VII: −9x+my=−4 mx−y=m |−9 m| m −1 |=W 9−m²=W stad ze by uklad mial rozwiazanie to W≠0 stad m≠3 i m≠−3

qTarantin0: Ale dlaczego przedział zaczyna się od −3 skoro m≥−1?

ICSP: W = 9 − m² W_x = 4 − m² W_y = −5m

	m2 + 5m − 4
x + y =
	m2 − 9

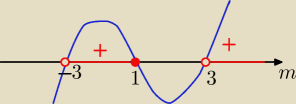
x + y ≥ 1 (m+1)(m−3)(m+3) ≥ 0 m ∊ (−3 ; −1> ∪ (3 ; ∞)

qTarantin0: Dziękuję

Eta: W= −m²+9 ≠0 ⇒ m≠3 i m≠ −3 W_x= −m²+4 W_y= −5m

	m2−4		5m
x=		i y=
	m2−9		m2−9

x+y≥1

	m2−9+5m−m2+9
		≥0
	m2−9

5(m+1)(m−3)(m+3)≥0 Odp: m∊(−3,1> U (3, ∞) =================

qTarantin0: Dziękuję