Założenia równania krzyś: Dane jest równanie x²−5mx+4m=0 Wyznacz zbiór wszystkich wartości parametru m, dla których oba rozwiązania tego równania są mniejsze od 10. założenia: wiem, że Δ > 0, ale kompletnie nie rozumiem z czego wynika f(10) > 0 i x_w < 10 proszę o pomoc i wyjaśnienie!

ICSP: Takie rzeczy zazwyczaj odczytujesz z interpretacji wykresu funkcji kwadratowej. Δ > 0 x_w < 10 ⇒ x₁ < x_w < 10 i x₂ > x_w (ale nie koniecznie musi być mniejsze od 10) f(10) > 0 ⇒ x_w < x₂ < 10 Ponieważ nie możesz z liczb ujemnych przejść na liczby dodatnie nie wykonując skoku.

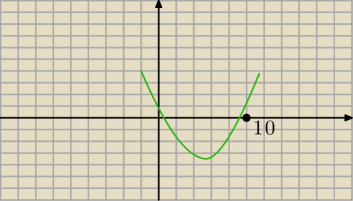
Jerzy: A ten rysunek ci wyjaśnia te warunki ?

chichi: Dlatego, że a>0 zatem parabola ma ramiona skierowane w górę, (x_w<0) więc wysuwamy wierzchołek w lewo od 10, dzięki temu mamy pewność, że mniejsze miejsce zerowe przebije oś OX przed 10, ale wciąż to większe może przebić za 10, więc jeśli f(10)>0 to oznacza, że przebije oś OX również przed 10. No i mamy spełnione warunki zadania. Narysuj sobie na kartce

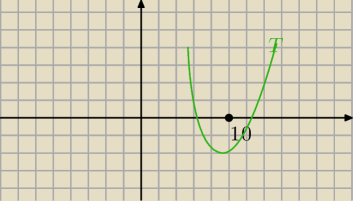
Jerzy: Tutaj mamy x_w < 10 , ale f(10) < 0 , czyli tylko jeden pierwiastek jest mniejszy od 10

chichi: Zastanów się co gdyby współczynnik 'a' byłby sparametryzowany

krzyś: Dziękuję ogromnie za odpowiedzi! Myślę, że w przyszłości nie będę miał z tym problemu! A gdyby współczynnik 'a' był sparametryzowany to dla a=0 nie byłoby dwóch rozwiązań, bo równanie nie byłoby kwadratowe, a gdyby a<0 to f(10)<0. Dobrze rozumuję? O to chodziło?