Stożek Stożeczek: W kulę o promieniu R wpisano stożek. Jaki musi być promień podstawy ( w odniesieniu do R), aby pole powierzchni bocznej stożka było największe

kerajs:

	2√2
Postawię na: r=		R
	3

Filip: Cześć kerajs, co stawiasz?

kerajs: Siemasz. Stawiam to co zwykle, czyli kiepską reputację.

Mila: No to napisz , jak to liczyłeś

Eta: Hej Mila Też mam taką odpowiedź

jc: Tak samo.

chichi: Autor i tak już chyba zapomniał

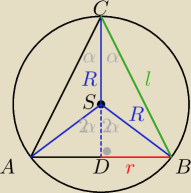
Minato: α ∊ (0, 90) P(r,l) = πrl W ΔSDB

	r
sin(2α) =		⇒ r = Rsin(2α) = 2Rsinαcosα
	R

W ΔCDB

	r		r		Rsin(2α)
sinα =		→ l =		=		= 2Rcosα
	l		sinα		sinα

P(α) = π*2Rsinαcosα*2Rcosα = 4πR²sinαcos²α = = 4πR²sinα(1−sin²) = 4πR²(sinα − sin³α) P'(α) = 4πR²(cosα − 3sin²αcosα) = 0 cosα−3sin²αcosα = 0 cosα(1−3sin²α) = 0

	1
cosα = 0 lub sin2α =
	3

	√3
sprzeczność, bo α∊(0, 90) lub sinα =
	3

[UWAGA: należy sprawdzić czy faktycznie w tym punkcie jest maksimum] Doliczamy cosα z jedynki trygonometrycznej

1
	+ cos2α = 1
3

	√6
cosα =
	3

	√3		√6		2√2
r = 2R*		*		=		R
	3		3		3