powinowactwo nieogar: Jak wygląda wzór funkcji: y=sin(x−π/2)+1 w powinowactwie prostokątnym o osi X i skalach 4 oraz 1/5 y=cos(−x) w powinowactwie prostokątnym o osi Y i skalach 2 oraz 1/2

6latek: Powinowactwo prostokatne o osi 0X i skali k Wzor y=k*f(x) dla k>1 uzywamy pojecia rozciagania wykresu k razy wzdluz osi OY dla 0,k<1 uzywamy pojecia sciskania wykresu k razy wzdluz osi 0Y Powinowactwo prostokatne o osi OY i skali k y=Wzor y=f(k*x) dla k>1 uzywamy pojecia sciskania wykresu k razy wzdluz osi OX

	1
dla 0<k<1 uzywamy pojecia rozciagania wykresu		razy wzdluz osi OX
	k

6latek: Jak rozumiesz pojecie osi X?

nieogar: Rozumiem powinowactwo o osi X tak, że rozciągamy wykres w pionie 4sin(x−π/2)+1 /rozciągamy/ 1/5sin(x−π/2)+1 /ściskamy/ o osi Y cos(−2x) /ściskamy w poziomie/ cos(−1/5x) /rozciągamy w poziomie/ Dobrze, czy bzdura?

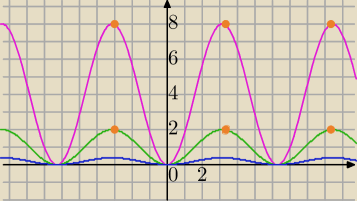
Mila: 1) y=sin(x−π/2)+1 w powinowactwie prostokątnym o osi X i skalach 4 oraz 1/5 Jeżeli wykres funkcji y=f(x) przekształcamy przez powinowactwo prostokątne o osi OX i skali k≠0, to otrzymamy wykres funkcji y=k*f(x).

	π
f(x)= sin(x−		)+1 − zielony wykres
	2

Przekształcenie: k=4, powinowactwo prostokątne o osi OX

	π
g(x)=4*(sin(x−		+1)
	2

	π
g(x)=4*sin(x−		)+4 − różowy wykres
	2

	1
2) k=		, powinowactwo prostokątne o osi OX
	5

wzór

	1		π		1
y=		sin(x−		)+		− niebieski wykres
	5		2		5

nieogar: Dzięki. Postaram się to przeanalizować. Pozdrawiam serdecznie

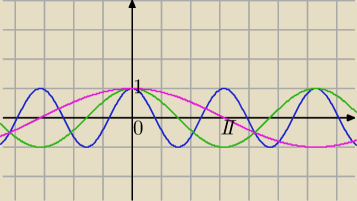
Mila: 2) Jeżeli wykres funkcji y=f(x) przekształcamy przez powinowactwo prostokątne o osi OY i skali k≠0,

	1
to otrzymamy wykres funkcji g(x)=f(		*x)
	k

==================================] y=cos(−x) , cos(x) jest funkcją parzystą⇔ f(x)=cos(x), 1) k=2, powinowactwo prostokątne o osi OY

	1
g(x)=cos(		x) zielony wykres "rozwleka się"− różowy ( ucieka od osi OY )
	2

	2π
okres: T=		=4π
	1   2

2)

	1
k=		, powinowactwo prostokątne o osi OY
	2

wzór: g(x)=cos(2x) − − wykres "biegnie" do osi OY

	2π
okres: T=		=π
	2

−)

	1
zbiór wartości w obu przypadkach ( k=2 i k=		i powinowactwo prostokątne o osi OY)
	2

zostaje ten sam, jak dla funkcji f(x).

nieogar: Chyba już ogarniam. Bardzo dziękuję za poświęcony czas.

Mila: