Geometria
Rumcajs72: W trójkącie ABC wysokość BD=6, środkowa CE=5, a odległość punktu przecięcia się odcinków
BD i CE od boku AC=1. Oblicz AB.
7 sty 22:12
7 sty 22:47
Rumcajs72: Tak dobry a jak to policzyłeś
7 sty 22:50
chichi:
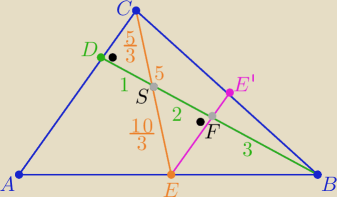 (1)
(1)
|DS|=1 ∧ EE' ∥ AC
|DF|=|FB|=3 ⇒ |SF|=2
(2)
| | 1 | |
ΔDCS∼ΔKEP (w skali k= |
| ) |
| | 2 | |
| | 5 | |
(|CS|=x ⇒ |SE|=2x) ⇒ 3x=5 ⇒ x= |
| , zatem: |
| | 3 | |
(3)
Twierdzenie Pitagorasa dla ΔSFE:
| | 10 | | 8 | |
22+|EF|2=( |
| )2 ⇒ |EF|= |
| |
| | 3 | | 3 | |
(4)
Twierdzenie Pitagorasa dla ΔBFE:
| | 8 | | √145 | |
32+( |
| )2=|EB|2 ⇒ |EB|= |
| |
| | 3 | | 3 | |
(5)
|AB|=2|EB|
8 sty 01:22
chichi:
Mała korekta
 (2)
(2)
| | 1 | |
ΔDCS∼ΔFES (w skali k= |
| ) |
| | 2 | |
Już tak późno, a przepisuje z kartki, a tu miałem inne oznaczenia więc wkradł się chochlik

8 sty 01:25
a@b:
@
chichi
Bardzo ładnie wytłumaczone : "kawa na ławę",tylko
ciasteczka brak


8 sty 14:50
a@b:
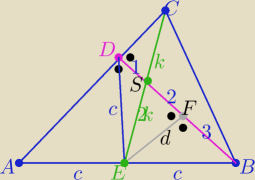
Też podobnie jak u Ciebie
chichi
w ΔDEF : c
2=d
2+9 i w ΔSEF : d
2=4k
2−4
| | 100 | | 45 | |
to c2=4k2+5 ⇒ c2= |
| + |
| |
| | 9 | | 9 | |
=================
8 sty 15:03
chichi:
Dziękuję! @
Eta Na forum zawsze wrzucam takie szczegółowe rozwiązania, żeby później nie
odpowiadać na pytania: "a skąd to?", "a dlaczego tak?" etc.
Gdybym rozwiązanie robił dla Ciebie czy osoby obytej z geometrią, to pewnie poza rysunkiem 2−3
linijki i pojawiłby się wynik

8 sty 15:15
 (1)
|DS|=1 ∧ EE' ∥ AC
|DF|=|FB|=3 ⇒ |SF|=2
(2)
(1)
|DS|=1 ∧ EE' ∥ AC
|DF|=|FB|=3 ⇒ |SF|=2
(2)
 (2)
(2)



 Też podobnie jak u Ciebie chichi
Też podobnie jak u Ciebie chichi
