Geometria Rumcajs72: W trójkącie ABC na linii średniej M₁M₂ równoległej do AB jako na średnicy zbudowano okrąg, który przecina boki AC i BC w M i N. Oblicz MN, jeśli AB=c, AC=b i BC=a.

Mila:

	c
|M1M2|=
	2

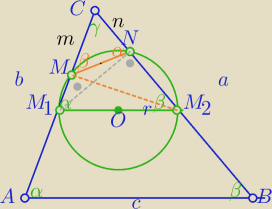
1)Czworokąt M₁M₂NM wpisany w okrąg ⇔ ΔMNC∼ΔM₁M₂C⇔

	1
ΔM1M2∼ΔABC w skali k=
	2

m		a		c
	=		⇔|MN|=m*
MN		c		a

	MM1
2) W ΔM1M2M: cosα=
	1   c 2

	1
|MM1|=		c*cosα
	2

	1		1		1
m=		b−		c*cosα=		(b−c cosα)
	2		2		2

	b2+c2−a2
cosα=
	2bc

	1		b2+c2−a2		1		b2+c2−a2
m=		*(b−c*		)=		*(b−		)
	2		2bc		2		2b

	a2+b2−c2
m=
	4b

3)

	c		a2+b2−c2
|MN|=		*
	a		4b

	c*(a2+b2−c2)
|MN|=
	4ab

======================

chichi: O to już nawet nie wrzucam, bo rozwiązanie to samo no chyba, że wpadnę na inny pomysł

kerajs: Ja rozwiązywałem z trójkąta MON, gdzie kąt MON = 180^*−2γ .

Mila: Może kerajsik ma inne?

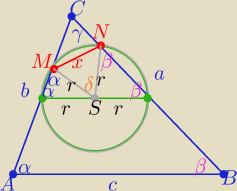
a@b: r=c/4 δ=180^o−2γ cosδ= −cos(2γ) Z tw. kosinusów w ΔMSN x²=r²+r²+2r²cos(2γ) x²= 2r²(1+cos(2γ)) = 2r²*2cos²γ

	a2+b2−c2
x=2rcosγ i cosγ=
	2ab

	c(a2+b2−c2)
x=
	4ab

================

chichi:

kerajs:

	c		c		a2+b2−c2		c(a2+b2−c2)
|MN|=2|OM|cos(∡{NMO})=2		cos γ=				=
	4		2		2ab		4ab

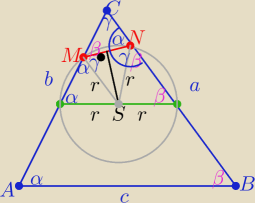
a@b: No to ...."pojechałam na wycieczkę z tw. Carnota" teraz dopiero widzę,że α+β+γ=180^o to |∡NMS|=|∡MNS|=γ

	x/2		x
to cosγ=		=
	r		2r

	c		a2+b2−c2
x=2rcosγ =		*
	2		2ab

	c(a2+b2−c2)
x=
	4ab

==============

chichi: @Eta Nie mów tak publicznie, bo jeszcze policja cię odwiedzi za tę wycieczkę

a@b: Mogę,bo jestem zaszczepiona

ite: to jeszcze gorzej, odwiedzi Cię CBŚ, dziennikarze i parę stacji telewizyjnych...

a@b: No i będę celebrytą A po za tym,to jestem z grupy 70+

ite: na tym forum już jesteś celebrytką!

a@b:

chichi: Cześć @ite to prawda @Eta tutaj już jest celebrytką. Miłego weekendu drogie Panie

ite: Dziękuję, ale nie wiem, jaki to będzie weekend. Może po tej wymianie zdań obie spędzimy go w tej samej celi. Chyba że moderatorzy zainterweniują.

a@b: Spokojnie ite