przestrzenie liniowe asd: Sprawdzic czy dany zbior jest podprzestrzenia przestrzeni R³(R) V = {(a,b,c)∊R³:a*b = 0} W≠0,bo (0,0,0)∊W Niech x,y ∊ W x = (a,b,c) ∊ R³:a*b = 0 * y = (a₂,b₂,c₂) ∊ R³:a₂*b₂ = 0 ** x+y = (a+a₂,b+b₂,c+c₂) No pierwsze zalozenie to ∀ x+y ∊ W x,y∊W To co mam tu sprawdzić,czy a+a₂ ∊ V? Nie wiem jak wykorzystać warunki * i ** tutaj. A w zasadzie nie wiem co sprawdzić. Tak samo drugi warunek Niech x ∊ V i α ∊ R,czyli α*x = (α*a,α*b,α*c) i sprawdzam,czy α*a = 0? Nie widzę w tym zastosowania tych warunków * i ** co zapisałem u góry,więc tak jak pisałem − nie wiem co sprawdzić

asd: V ≠ 0, bo(0,0,0) ∊ V,kolizja oznaczen jak sie ma innego cwiczeniowca i wykladowce

jc: (1,0,0) ∊V, (0,1,0) ∊V, ale (1,0,0)+(0,1,0)=(1,1,0) nie należy do V. V nie jest podprzestrzenią.

asd: Dziękuje za odpowiedź,ale nie do końca to rozumiem który wektor jest który i jakie działania między jakimi wektorami zostały wykonane

asd: No i to co Pan/Pani sprawdził

jc: podzbiór V przestrzeni W jest podprzestrzenią W, jeśli suma dowolnych dwóch wektorów z V należy do V iloczyn dowolnego wektora z V i dowolnej liczby należy do V (dodaje się zwykle, że V nie jest zbiorem pustym) Aby pokazać, że V nie jest podprzestrzenią, wskazałem daw wektory z V, których suma nie należała do V.

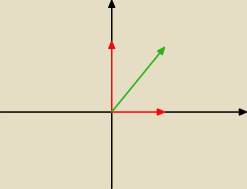
jc: Zapomnij o 3 współrzędnej. Rozpatrywany zbiór, to suma osi (czarne linie). Suma dwóch wektorów, jeden z jednej linii, drugi z drugiej (czerwone strzałki) nie leży na żadnej z czarnych linii (sumę oznaczyłem zieloną strzałką).

asd: dziękuje