Warunki dystrybuanty matematyk: Jakie warunki muszą spełniać liczby rzeczywiste a, b, c, d, żeby funkcja określona wzorem:

	⎧	0 dla x < 0
F(x) =	⎨	ax+b dla 0 <= x <= 1
	⎩	c + dx

a) była dystrybuantą pewnego rozkładu b) dystrybuantą pewnego rozkładu ciągłego wyszło mi c = 1 oraz oraz a, b, d > 0 czy da się to jakoś bardziej ograniczyć? Dla podpunktu b: a + b = 1, bo funkcja musi być ciągła. Czy mógłby ktoś podpowiedzieć czy to jest dobrze i ewentualnie nakierować?

Qulka: b=0 żeby dla x=0 było 0 więc a=1

matematyk: I to wszystko w tym zadaniu ?

matematyk: Odświeżam pytanie, bo jednak nadal nie rozumiem jak zrobić to zadanie, czy ktoś mógłby wytłumaczyć?

Qulka: c=1 i d=0 żeby potem niezależnie od x było 1

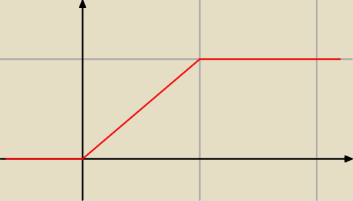
Qulka: wykres dystrybuanty

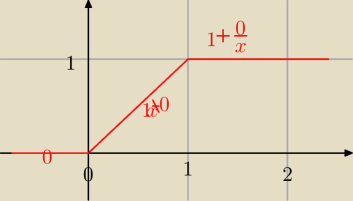
Qulka: czyli wszystko razem a=1 b=0 c=1 d=0

Qulka: tam na skosie miało być 1x+0

matematyk: Tak to rozumiem, tylko, że to jest dla przypadku, gdy mamy do czynienia z rozkładem ciągłym ? A co jeżeli mamy dowolny rozkład? Czy wtedy otrzymamy po prostu c = 1, d = 0 i a,b > 0?