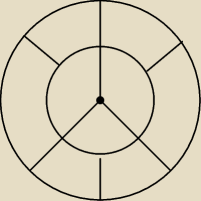
Lemat Burnside'a xxx: Na ile różnych sposobów można pokolorować 3 obszary na czerwono i 6 obszarów na biało? 2 pokolorowania różniące się tylko dowolną izometrią uznajemy za identyczne.

Adamm: G = S₃ = D₆ X to zbiór różnych pokolorowań (bez dokładności do izometrii) |X/G| to szukana liczba różnych pokolorowań z lematu Burnside'a

	1		1
|X/G| =		∑g∊G |Xg| =		∑g∊G |Xg|
	|G|		6

gdzie X^g to zbiór elementów x∊X dla których g(x) = x mamy 3 symetrie s₁, s₂, s₃ oraz 3 obroty o₁ = Id, o₂, o₃ |X^s₁| = |X^s₂| = |X^s₃|, |X^o₂| = |X^o₃|, |X^o₁| = |X|

	9 3		9 6
|X| =		+		= 84,

	3 2		3 1
|Xo2| =		+		= 6

	4 3		4 1
|Xs1| =		+		= 8

	84+2*6+3*8		120
Czyli jak dobrze policzyłem, to |X/G| =		=		= 20
	6		6

xxx: Zrozumiałem, dziękuję!

dobra_rada:

	5 3		5 2
Czy w symetrii nie powinno być		+		?

dobra_rada: Jednak nie − namieszałem − Adamm ma racje