. Mil: Obliczyć za pomocą całki oznaczonej pola figur ograniczonych liniami, wykonać rysunki, zaznaczyć obliczane pola a) 𝑦 = pierwiastek z 8x, 𝑦 =2/3(𝑥 + 4), b) 𝑦 = ln 𝑥, 𝑦 = −1, styczna do wykresu funkcji 𝑦 = ln x w punkcie 𝑥 = 1, c) 𝑥𝑦 = 1, 𝑥𝑦 = 8, 𝑦 = 𝑥², 𝑦 =1/8𝑥², d) 𝑦 = 𝑥² − 𝑥 − 6, 𝑦 = −𝑥² + 5𝑥 + 14. Jak to zrobić? W jakiej kolejności zrobić co i jak, powie ktoś? Nie miałam takiego zadania i nie umiem go zrobić

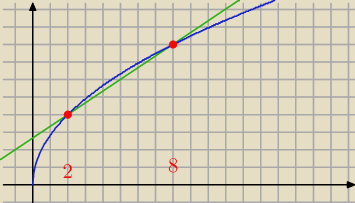Qulka: √8x=2(x+4)/3 to x=2 lub 8 8

	2√8x3−x2−8x		2•64−82−8•8		2•8−22−8•2
∫√8x−2(x+4)/3 =		]28 =		−		=4/3
	3		3		3

2

Mil: A skąd wiadomo ile jest rowny x? Jak to obliczyc? To jest wzór mnozenia czy jak?

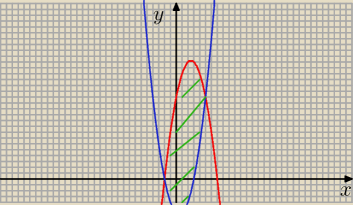
janek191: d) y = x² − x − 6 y = − x² + 5 x + 14 Wyznaczamy punkty wspólne: x² − x − 6 = − x² + 5 x + 14 2 x² − 6 x − 20 = 0 / : 2 x² −3 x − 10 = 0 Δ = 9 − 4*1*(−10) = 49 √Δ = 7

	3 − 7
x1 =		= − 2
	2

x₂ = 5 Pole 5 P = ∫ (−x² + 5 x +14 − ( x² − x − 6)] dx = ∫(−2 x² +6 x +20) dx = −2*∫ ( x² −3 x −10) dx= − 2

	1		3
=−2* [		x3 −		x2 − 10 x ] w granicach −2 do 5
	3		2

	1		3		1		3
=− 2*[		*125 −		*25 − 50 − (		*(−8) −		*4 +20)] =
	3		2		3		2

Podopisuj granice całkowana i dokończ obliczenia

Qulka: rozwiązać to równanie pierwsza = druga (y=y) √8x=2(x+4)/3 lub narysować staranny rysunek i odczytać gdzie się przecinają

Mil: Ale ja próbowałam rozwiązać a i mi nie wychodziło i nie wiem czemu

Qulka: razy 3 i do kwadratu 9•8x=4(x+4)² x²−10x+16=0 Δ=36 x₁=2 x₂=8

Mil: A czemu tak akurat?

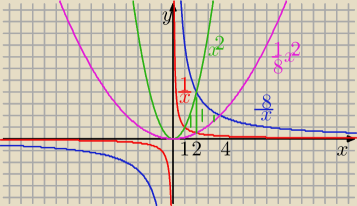
janek191: Rysunek do c)

janek191: c)

	1
y =		y = x2
	x

1
	= x2 / *x
x

1 = x³ x = 1 −−−−−−−−−

	8
y =		y = x2
	x

8
	= x2 / 8x
x

8 = x³ x = 2 −−−−−−−−−−

	1		1
y =		y =		x2
	x		8

1		1
	=		x2 / 8x
x		8

8 = x³ x = 2 −−−−−−−−−−

	8		1
y =		y =		x2
	x		8

8		x2
	=		/ * 8x
x		8

64 = x³ x = 4 −−−−−−

janek191: Pole 2 4

	1		8		x2
P = ∫ [ x2 −		]dx + ∫ [		−		] dx =
	x		x		8

1 2

Qulka: w a) ponieważ chciałam się pozbyć mianownika i pierwiastka dlatego tak

janek191:

	1
y = ln x ⇒ y ' =
	x

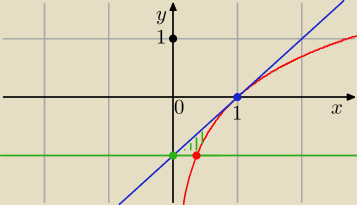
y = − 1 Dla x = 1 y ' = 1 ln 1 = 0 Mamy y = 1*x + b 0 = 1 + b ⇒ b = − 1 y = x − 1 równanie stycznej do krzywej y = ln x w punkcie x = 1. Punkty wspólne: y = − 1 i y = x − 1 −1 = x − 1 x = 0 −−−−−−− ln x = − 1 ⇒ x = e⁻¹ −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− y = x − 1 i y = ln x x − 1 = ln x x = 1 −−−−−−−−−−− Pole 1/e 1 P = ∫ [ x − 1 − ( − 1) ] dx + ∫ [ x − 1 − ln x ] dx = 0 1/e

Mil: A wiecie może jak zrobić przykład b?

janek191: Patrz 21.58

janek191: ∫ ln x dx = x*ln x − x + C

Mil: Ślicznie dziękuję wszystkim