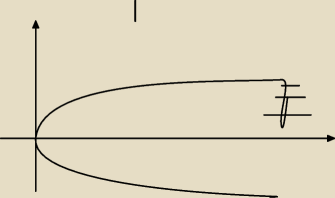
 obliczyc pole ograniczone lukiem paraboli y2=2x i prosta x=8
i mam problem z narysowniem tej paraboli bo mi caly czas wydaje sie ze to bedzie tylko ramie
nad osia ox, a wksiazce jest cos takiego bez tego fragemntu skreslonego, bo nie umialam go
zgumowac
moze mi ktos wyjasnic jak narysowac taka parabole
obliczyc pole ograniczone lukiem paraboli y2=2x i prosta x=8
i mam problem z narysowniem tej paraboli bo mi caly czas wydaje sie ze to bedzie tylko ramie
nad osia ox, a wksiazce jest cos takiego bez tego fragemntu skreslonego, bo nie umialam go
zgumowac
moze mi ktos wyjasnic jak narysowac taka parabole
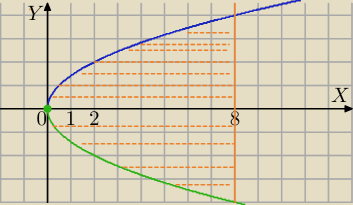
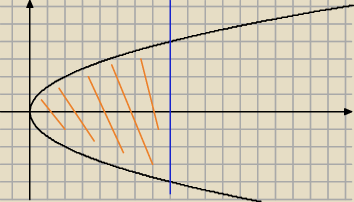 czarna − parabola
niebieska − prosta x = 8
pomarańczowe − pole którego szukasz = 2 * ∫08 √2x dx
czarna − parabola
niebieska − prosta x = 8
pomarańczowe − pole którego szukasz = 2 * ∫08 √2x dx
| 1 | ||
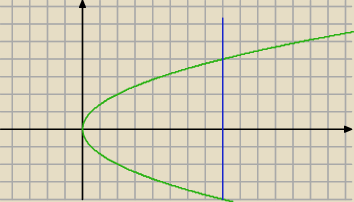
czyli jak chce rysowac to mam sb przeksztalcic do postaci x= | y2 wtedy normalnie widze | |
| 2 |
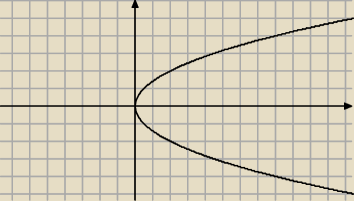 Drugie sobie dorysuj recznie .Odbij symatrycznie wzgledem osi OX
Albo pisz sobie do kratki y=−√2x
Drugie sobie dorysuj recznie .Odbij symatrycznie wzgledem osi OX
Albo pisz sobie do kratki y=−√2x
 aaa
Mialem Ci nie odpisywac ale dobra odpisze CI na twoj post 14 : 59
Nie byloby pytania z 13 :52 (skad sie bierze ta czesc wykresu pod osia OX ) gdyby bylo wiadomo
co to jest parabola
Parabola to nie tylko wykres funkcji kwadratowej ale takze
Parabola jest zbiorem wszystkich punktow rowno odleglych od jej ogniska i jej kierownicy
Punkty takie wyznacza sie konstrukcyjnie (wiadomo jak )
Wiec wykres y2=2x mozna narysowac bez programu rysujacego i kalkulatora . Tak rysowalem i to
na papierze milimetrowym
aaa
Mialem Ci nie odpisywac ale dobra odpisze CI na twoj post 14 : 59
Nie byloby pytania z 13 :52 (skad sie bierze ta czesc wykresu pod osia OX ) gdyby bylo wiadomo
co to jest parabola
Parabola to nie tylko wykres funkcji kwadratowej ale takze
Parabola jest zbiorem wszystkich punktow rowno odleglych od jej ogniska i jej kierownicy
Punkty takie wyznacza sie konstrukcyjnie (wiadomo jak )
Wiec wykres y2=2x mozna narysowac bez programu rysujacego i kalkulatora . Tak rysowalem i to
na papierze milimetrowym  Teraz mozna narysowac sobie w programie i to nie wedlug mnie nie jest zle . Po to sa
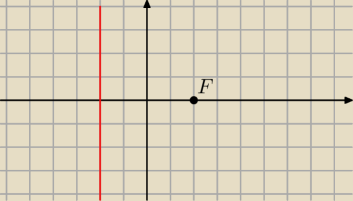
Mamy rownanie y2=8x czyli y2=2*4x stad p=4 stad F=(2,0) i rownanie kierownicy
x=−2(czerwona)
Teraz mozna narysowac sobie w programie i to nie wedlug mnie nie jest zle . Po to sa
Mamy rownanie y2=8x czyli y2=2*4x stad p=4 stad F=(2,0) i rownanie kierownicy
x=−2(czerwona)
 y2=2x
prosta x=8
Aniu
y2=2x to równanie paraboli , której osią symetrii jest oś OX,
z równania widać, że 2x≥0, ale y ∊(−∞,∞)
y2=2x − wykres nie jest wykresem funkcji
2) Jeżeli chcesz narysować wykres w układzie XOY, to robisz to w dwóch etapach:
y=√2x
lub
y=−√2x
3) Ponieważ obszar nie jest normalny względem OX, a OX jest osią symetrii obszaru,
to pole masz obliczone wg wzoru:
P= 2 *0 ∫8 √2x dx=2√20∫8√x dx=...?
Oblicz , a pokażę Ci inny sposób.
y2=2x
prosta x=8
Aniu
y2=2x to równanie paraboli , której osią symetrii jest oś OX,
z równania widać, że 2x≥0, ale y ∊(−∞,∞)
y2=2x − wykres nie jest wykresem funkcji
2) Jeżeli chcesz narysować wykres w układzie XOY, to robisz to w dwóch etapach:
y=√2x
lub
y=−√2x
3) Ponieważ obszar nie jest normalny względem OX, a OX jest osią symetrii obszaru,
to pole masz obliczone wg wzoru:
P= 2 *0 ∫8 √2x dx=2√20∫8√x dx=...?
Oblicz , a pokażę Ci inny sposób.
 tylko kto dziś wie co to kierownica ognisko i po co to i do czego .. więc
dziewczynie tylko zamąciłeś zamiast pomóc
tylko kto dziś wie co to kierownica ognisko i po co to i do czego .. więc
dziewczynie tylko zamąciłeś zamiast pomóc  i chodziło mi o to żeby się nie stresowała Twoim
wpisem, który w obecnych czasach jest dla nich niezrozumiały
i chodziło mi o to żeby się nie stresowała Twoim
wpisem, który w obecnych czasach jest dla nich niezrozumiały 
 Pozdrawiam
Pozdrawiam 