algebra liniowa Filip: Witam, prosilbym o sprawdzenie ponizszych zadan(ew rozwiazania w przypadku bledu) Zad 1 Przez punkt P(1,4−3) poprowadzic prosta przecinajaca prosta l: x=2t i y=3−t, z=2+t, t∊R pod katem prostym

	3		11
l: x=1−2t i y=2−		t i z=−4−		t
	4		2

Zad 2 Przez punkt A(1,−1,1) poprowadzic plaszczyzne prostopadla do plaszcyzny π₁: x−y+z−1=0 i π₂:2x_yz1=0 π_⊥: −2x+y+3z=0 Zad 3 znalezc kat miedzy miedzy prosta l: 3x−2y=24 i 3x−z=−4 a plaszczyzna π₀: 6x+15y−10z+31=0 α≈74^o

Mila: W (1) pomijając prostopadłość ,punkt (1,4,−3) nie należy do prostej, której równanie podałeś. (3) mam inny kąt . Jaki masz sin kąta między wektorem kierunkowym prostej i wektorem normalnym płaszczyzny ? (2) tam masz równanie krawędziowe prostej x−y+z−1=0 i 2x=0 ? Czy x−y+z−1=0 i 2x+y+z+1=0

Filip: Zadanie 2 2x+y+z+1=0 W takim razie, czy moglabys zamiescic swoje rozwiazania z komentarzami? Bardzo prosze

Mila: Zadanie (1) 1) P(1,4,−3) Prosta: l: x=2t y=3−t, z=2+t, gdzie t∊R k⁼[2,−1,1] −wektor kierunkowy prostej l 2) m⊥l i P∊m P'− Rzut prostokątny punktu P na prostą l; P'=(2t,3−t,2+t) PP'^→=[2t−1, 3−t−4,2+t+3] =[2t−1,−t−1,t+5]⊥k^→⇔ [2t−1, −t−1,t+5] o [2,−1,1]=0⇔ 2*(2t−1)+(−1)*(−t−1)+1*(t+5)=0

	2
t=−
	3

	7		1		13
PP'→=[−		,−		,		] || [7,1,−13]
	3		3		3

k^1→=[7,1,−13]− wektor kierunkowy prostej m (spr. ⊥) [7,1,−13]o [2,−1,1] =0 m: P(1,4,−3 ) ∊m

x−1		y−4		z+3
	=		=
7		1		−13

albo x=1+7s y=4+s z=−3−13s, gdzie s∊R ================ JC może spojrzy i poda Ci krótszy sposób.

Mila: Zadanie 2) Masz dobrze. Przez punkt A(1,−1,1) poprowadzić płaszczyznę prostopadłą do płaszczyzny π₁: x−y+z−1=0 i π₂: 2x+y+z+1=0 n₁=[1,−1,1], n₂=[2,1,1] n₁ x n₂=[1,−1,1] x[2,1,1]= [−2,1,3] || [2,−1,−3] n^→= [2,−1,−3]− wektor normalny szukanej płaszczyzny ==================== π⊥π₁ i π⊥π₂ π: 2*(x−1)−(y+1)−3*(z−1)=0 π: 2x−y−3z=0

Mila: zadanie 3) Napisz jak liczyłeś.

Filip: Tak, zadanie pierwsze inaczej troche liczyles, ale tez teraz sie zorentowalem, ze podalem zle wspolrzedne punktu P, powinno byc P=(1, 2, −4) Zadanie 3 liczylem tak: n₁^→=[1,−1,1] n₂^→=[2,1,1] n₁^→ x n₂^→ = [2,6,6]=v^→ u^→=[6,15,01]

	v→ o u→
cosα=
	|v→|*|u→|

Mila: Znaleźć kąt miedzy między prostą l: 3x−2y=24 i 3x−z=−4 a płaszczyzną π₀: 6x+15y−10z+31=0 n^→=[6,15,−10]− wektor normalny płaszczyzny 1) k^→=[3,−2,0] x [3,0,−1]=[2,3,6] − wektor kierunkowy prostej l α− jest kątem ostrym między wektorem normalnym płaszczyzny i wektorem kierunkowym prostej

	π
φ=		−α − Kąt między prostą a płaszczyzną w R3
	2

	|k x n| ]
sinα=
	|k|*|n|

licz teraz.

Filip: Przepraszam, pomieszaly mi sie cyfry, oczywiscie liczylem tak jak ty, jednak wektor kierunkowy prostej l, wspolrzedna y wyszla mi 6 I dlaczego liczymy sinus zmiast cosinusa?

jc: Te same rachunki, co u Mili, ale trochę inne spojrzenie. Rysujemy płaszczyznę prostopadłą do prostej (x,y,z)=(0,3,2) + t( 2, −1, 1) przechodzącą przez punkt (1,4,−3): 2x−y+z=d=2−4−3=−5 Teraz znajdujemy przecięcie płaszczyzny z prostą: 2(2t)−(3−t)+(2+t)=−5 6t=−4, t=−2/3 punkt przecięcia = (0,3,2) − (2/3)(2,−1,1) =(−4/3, 11/3, 4/3) Wektor kierunkowy szukanej prostej: (−4/3, 11/3, 4/3) − (1, 4,−3)=(−7/3, −1/3, 13/3) || (7,1,−13) Szukana prosta (x,y,z) = (1,4,−3) + t(7,1,−13). −−−− Niedawno na forum było zadanie w którym należało sprawdzić, że wektor u jest prostopadły do wektora u² v − u*v u. Można było wykorzystać ten wzór biorąc u=(2,−1,1), v=(1,4,−3)−(0,3,2)=(1,1,−5). Wzór daje wektor 6(1,1,−5) + 4(2,−1,1) = (14,2,−26) = 2 (7,1,−13)

Mila: Dziękuję

Filip: Dzieki za rozwiazanie, znajomy podal mi inne i jestem ciekaw czy tez jest poprawne. Pierw wyznaczam wektor rownolegly do prostej l −> z tego dostaje plaszczyzne prostopadla do prostej l oraz przechodzaca przez punkt P Nastepnie licze punkt przeciecia prostej l z plaszczyzna No i pozniej moge wyznaczyc wektor P, ktory bedzie rownolegly do szukanej prostej. Jesli jest to sposob poprawny to mam pytanie, skad wiemy, ze plaszczyzna ktora otrzymamy z wektora rownoleglego do prostej l bedzie pod katem prostym?

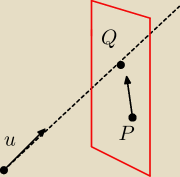
jc: To jest to samo, co ja napisałem. Spróbuję narysować. u = wektor kierunkowy prostej, linia przerywana = prosta czerwony kwadrat symbolizuje płaszczyznę prostopadłą do prostej przechodzącą przez punkt P. Prosta przecina płaszczyznę w punkcie Q. Wektor Q−P leży jest równoległy do płaszczyzny, a więc jest prostopadły do prostej.

Filip: Mila dlaczego zamiast cosinusa liczysz sinus? Czy w takim razie α≈14^o?

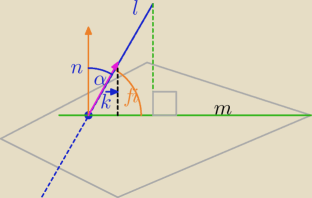
Mila: α− Kąt między wektorem kierunkowym prostej a wektorem normalnym płaszczyzny φ−kąt między prostą l a jej rzutem prostokątnym (m) na płaszczyznę W iloczynie wektorowym masz we wzorze sin kąta między wektorami

	π
Potem liczę: φ=		−α
	2

Jeśli zapiszemy:

	π
sin(		−α)=cosα
	2

zatem sinφ=cosα Możesz od razu napisać :

	|k x n|
cosα=
	|k|*|n|

Napisz treść zadania 3 jeszcze raz, bo inaczej mi wychodzi, a chcę Ci pokazać dwoma sposobami.

Filip: Tutaj tresc zadania 3 Znalezc kat miedzy miedzy prosta l: 3x−2y=24 i 3x−z=−4 a plaszczyzna π0: 6x+15y−10z+31=0 Jednak zakladam ze chodzilo ci o zadanie 2 , tresc: Przez punt A(1, −1, 1) poprowadzic plaszczyzne prostopadla do plaszcyzny π₁: x−y+z−1=0 π₂: 2x+y+z+1=0 Podrzucam jeszcze kolejne, z tym tez mialem problem: Zadanie 4 Znalezc wysokosc rownolegloscianu rozpietego przez wektory v₁=[1,3,7]^T, v₂=[−3,2,1]^T, v₃=[−2,−1,2]^T, poprowadzona na sciane rozpieta przez v₁ i v₂

jc: Rozwiązanie zadania 4.

	objętość		|v3 * (v1 x v2)|
h =		=
	pole podstawy		|v1 x v2|

Filip: jc dzięki, czyli zwykłe podstawienie do wzoru... Podrzucam kolejne, w wolnej chwili możesz spojrzeć: Znajdź odległość prostych skośnych

	x+1		y		z−1
l1=		=		=		i l2: x=t, y=−1+3t, z=2+4t, t∊R
	1		1		2

I tutaj też się nasuwa moje pytanie, jak interpretować zapis prostej l₁, pierwszy raz się z takim zapisem spotykam Pozdrawiam

jc:

x+1		y		z−1
	=		=		to taki staroświecki zapis.
1		1		2

x+1		y		z−1
	=		=		=t
1		1		2

x=t−1 y=t z=1+2t i masz już normalnie.