Potrzebuję pomocy w granicach ciągów sUser: Zadanie 1.Czy to jest dobre rozwiązanie?

	log3(3n+2)
limn−>∞		=
	log3 (9n+8)

	2   log33n * (1+ )   3n
= limn−>∞		=
	8   log39n * (1+ )   9n

	2   n * log33 + log3(1+ )   3n
= limn−>∞		=
	8   n * log39 + log3(1+ )   9n

	n * log33		2   log3(1+ )   3n
= lim		+ lim		=
	n * log39		8   log3(1+ )   9n

	log33		0		1
=		+		=
	log39		0		2

Zadanie 2.

	1		1
limn−>∞		+ ... +
	√n2+1		√n2+n

siedzę ponad godzinę i nie wiem jak zrobić to zadanie... Proszę o pomoc i z góry dzięki za zaangażowanie

Mila: Z tw. o trzech ciągach:

	1
Najmniejszy składnik :
	√n2+n

	1
Największy składnik:
	√n2+1

Składników jest n.

	1		n		1
an=n*		=		=		→1
	√n2+n		n*√1+1n		√1+1n

	1		n		1
bn=n*		=		=		→1
	√n2+1		n*√1+1n2		√1+1n2

	1		1		1		1		1
n*		≤		+		......+		≤n*		⇔
	√n2+n		√n2+1		√n2+2		√n2+n		√n2+1

	1		1		1
limn→∞		+		......+		=1
	√n2+1		√n2+2		√n2+n

Filip:

	0
Zadanie 1 − zle, zauwaz ze w pewnym momencie dostajesz		co jest symbolem nieoznaczonym,
	0

proponuje

	log3(3n+2)		inf
limn−>inf		=		− symbol nieoznaczony
	log3(9n+8)		inf

proponuje hospitalizowac

dlog3(3n+2)		3n
	=
dn		3n+2

dlog3(9n+8)		2*9n
	=
dn		9n+8

	log3(3n+2)		3n	9n+8		1
limn−>inf		=limn−>inf			=
	log3(9n+8)		3n+2	2*9n		2

Mila: Filip Nie możesz stosować reguły de l"Hospitala. Spróbuj z tw. o trzech ciągach.

Filip: dlaczego?

Mila: Pochodną liczymy dla funkcji ciągłej.

Filip: a funkcja f(n)=log₃(3ⁿ+2) ja nie jest?

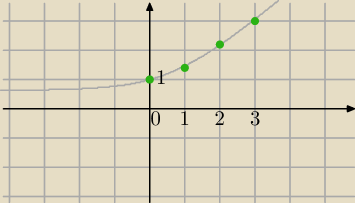
Mila: f(0)=log₃(3⁰+2)=1 f(1)=log₃(5) f(2)=log₃(11)

chichi: f: |N → |R jest ciągła

jaros: @Mila takie pytanko, skąd wypatrzyłaś największy i najmilejszy składnik do tw. o 3 ciągach?

Filip: Czyli jak to jest, finalnie nie mozna robic tego hospitalem?

chichi: √n²+n → +∞ zatem mianowniki będą co raz to większe i większe, a największym będzie właśnie √n²+n, licznik jest stały, a mianowniki rosną, czyli liczby maleją

chichi: @Filip musisz poczekać na ekspertów od analizy hah, ja póki co na analizie matematycznej mam granice ciągów prostszych niż w liceum byli I nie wiem kiedy ona się w końcu rozkręci na dobre Jeszcze niedawno Profesor zabraniał mi wchodzić z limesem pod pierwiastek, dopóki nie udowodnię, że pierwiastek jest funkcją ciągłą, więc no hah. W końcu to kierunek matematyka, zanim poznasz sposoby trzeba nabyć teorii i wszystko udowodnić

Mila: Jaros Nie pamiętam

sUser: Jak w takim razie rozwiązać zadanie pierwsze? nie bardzo mam pomysł na ograniczenia górne i dolne.

aaa: w pierwszym rozbijanie ułamka trochę nie tak

a+b		a		b
	≠		+		więc wcale tam nie ma 0/0
c+d		c		d

Filip: moze tak sUser

	log33n
an=
	log3(9n+8)

	log3(3n+2)
bn=
	log3(9n+8)

	log3(2*3n)
cn=
	log3(9n+8)

a_n<=b_n<=c_n

	log33n
limn−>infan=limn−>inf		=
	log3(9n+8)

	n		n		1
=limn−>inf		=limn−>inf		=
	8   log3(9n(1+ ))   9n		8   2n +log3(1+ )   9n		2

	log33n+log32
limn−>infcn=limn−>inf		=
	log3(9n+8)

	n+log32
=limn−>inf		=
	8   log3(9n(1+ ))   9n

	n+log32		1
=limn−>inf		=
	8   2n +log3(1+ )   9n		2

No i jak dla mnie teraz odpowiedni komentarz i koneic zadania, tylko sprawdz czy poprawnie dobralem ciagi

sUser: Filip, dzięki, napracowałeś się Mam tylko pytanie, ostatnia linia zadania, "n" nie jest wyłączone przed nawias w liczniku i mianowniku. Więc chyba nie można go tak poprostu skrócić (sam na początku zrobiłem ten błąd).

Filip: W ostatniej linijce patrzac na wyrazenie, zobaczylem, ze najwieksza potega zmiennej 'n' w liczniku jest taka sama jak najwieksza potega 'n' w mianowniku. Mozna tutaj podzielic licznik i mianownik przez n, albo mozna zobaczyc, ze jesli tak jest, to granica ciagu to bedzie iloraz wspolczynnikow stojacych przy tych 'n'.

	1
Tutaj w liczniku masz 1*n , a w mianowniku 2*n, wiec granica to bedzie
	2

Oczywiscie mozna jak mowisz, wyciagnac 'n' przed nawias:

	log32   n(1+ )   n
limn−>inf
	log3(1+8/9n)   n(2+ )   n

n sie skraca I napisac, ze

log32
	−> 0
n

log3(1+8/9n)
	−> 0
n

	1
wiec, g=		, jednak troche wiecej roboty jest, a nie jest to wymagane, wiec mozna na
	2

"skroty"

ICSP:

log33n		log3(3n+2)		log3(3n+2*3n)
	≤		≤
log3(9n+8*9n)		log3(9n+8)		log3 9n

n		n + 1
	≤ an ≤
2n + 2		2n

Z twierdzenia o trzech ciągach:

	1
lim an =
	2

jc: sUser, Wyłącznie nie ma sensu. Po wyłączeniu nadal nie możesz stosować twierdzenia o arytmetyce granic. Jeśli chcesz, to podziel licznik i mianownik przez n.

sUser: Już zrozumiałem. Dzięki wszystkim za pomoc. Pozdrawiam

Mila: Myślałam, że sUser lub Filip poda ograniczenia Miałam dzisiaj podać