. Sprawdź dla jakich x ∈ R zachodzi równość jaros: Sprawdź dla jakich x ∈ R zachodzi równość arctg(x) = arcctg({1}{x}) Nie mogę wpaść na pomysł jak rozwiązać ten problem

ICSP: Policz pochodną funkcji : f(x) = arctg(x) − arcctg(1/x)

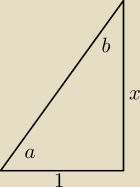
jc: arcctg 1/x = arctg x dla x>0. tg a = x ctg a = 1/x arctg x = a arcctg 1/x = 0 A jak będzie dla ujemnych x?

jaros: @ICPS pochodna tego wyrażenia jest równa 0, ale nie za bardzo wiem, jaki wniosek z tego wyciągnąć

jaros: @jc hmmm nie wiem za bardzo co masz na myśli, znaczy coś takiego tg b = −x?

jaros: @ICPS, @jc

ICSP: Skoro pochodna dla funkcji się zeruje to jaką postać ma ta funkcja?

jaros: no jest prostą w z dziedziną x ≠0

ICSP: prosta nie musi być funkcja. Jednak jesteś blisko.

jaros: Jednak nie wiem, gdzie teraz szukać

ICSP:

	⎧	A dla x > 0
f(x) =	⎨
	⎩	B dla x < 0

Wystarczy podstawić x = 1 aby sprawdzić ile wynosi A oraz x = −1 aby sprawdzić ile wynosi B.

jc: Oj, tam miało być arcctg 1/x=a, nie zero. arctg x = a oznacza, że x=tg a i a∊(−π/2, π/2) arcctg 1/x = a oznacza, że 1/x=ctg a, czyli x=tg a i a∊(0,π) Dlatego dla dodatnich x mamy równość. Dla ujemnych x, a<0, więc nie może być równości.

jaros: Tylko, że skąd wiemy, żeby przyjąć x=1 lub x=−1

ICSP: Skoro jest stała w przedziale x > 0 to nie ma różnicy którą liczbę z tego przedziału wezmę w celu obliczenia wartości funkcji f. Zacznij brać losowe liczby a zobaczysz dlaczego x = 1 jest wygodną.

Józef: Dla

	π		π
A dla x > 0, Prawda bo		=
	4		4

	π		3π
f(x) = B dla x<0, fałsz bo −		=
	4		4

Takie wnioski mają być?