trójkąt Kamil: Dany jest trójkąt ABC w którym dwusieczna kata BAD przecina bok BC w punkcie D tak,że AD=BD oraz AC=8, AB=10 Wyznacz stosunek obwodu okręgu wpisanego w ten trójkąt do obwodu okręgu opisanego na tym trójkacie

Filip: Przepisz poprawnie tresc zadania

Qulka: r=√7 R=16/√7

obwód w		7
	=
obwód o		16

a@b: Też tak mam

Kamil: Odpowiedzi to mam Jak do niej dojść ?

Filip: Nie da sie do niej dojsc, poniewaz tresc zadania jest zle przepisana. Powyzsze osoby tez nie wiem jak do niej doszli na podstawie takiej tresci

Qulka: Zmieniłam ∡BAD na ∡BAC

a@b: Ja też zobaczyłam BAC

Kamil: Przepraszam miał być kąt BAC

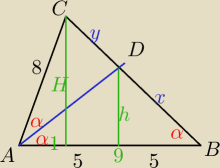
Qulka: z tw sinusów y=0,8x więc H=1.8h z tw Pitagorasa H=3√7 z tw Pitagorasa BC=12 r=2P(a+b+c) R=abc/4P

Qulka: no i oczywiście P=aH/2 = 15√7

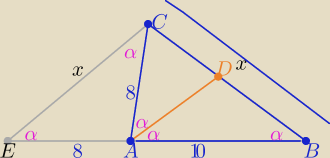
a@b: Z podobieństwa trójkątów równoramiennych EBC i EAC

x		8
	=		⇒ x=|BC|=12
8+10		x

Ze wzoru Herona P=..........=15√7 r=√7 R= 16/√7

r
	= .....
R