równ prostej tomcio: Czy tutaj brakuje danych? Punkty A=(1,1), B=(5,5), C=(3,5) są wierzchołkami trapezu równoramiennego ABCD niebędącego równoległobokiem, w którym ABIICD. a) wyznacz równanie osi symetrii tego trapezu b) oblicz pole tego trapezu Równanie osi symetrii z prostej AB obliczę, a co z prostą CD skoro nie ma danych wierzchołka D?

tomcio: Proszę o sprawdzenie, Czy tutaj brakuje danych? Punkty A=(1,1), B=(5,5), C=(3,5) są wierzchołkami trapezu równoramiennego ABCD niebędącego równoległobokiem, w którym ABIICD. a) wyznacz równanie osi symetrii tego trapezu b) oblicz pole tego trapezu Równanie osi symetrii z prostej AB obliczę, a co z prostą CD skoro nie ma danych wierzchołka D?

edi: Wiesz, że trapez jest równoramienny − to pozwala obliczyć wierzchołek D

edi: zresztą oś symetrii przedzieli na połowy zarówno podstawę AB jak i CD, również w ten sposób można wyliczyć D

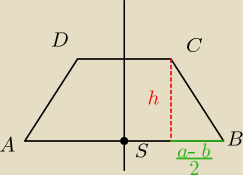
Godzio: D jest przecież nie potrzebne oś symetrii − prosta przechodząca przez środek odcinka AB i do niej prostopadła − z tymi danymi spokojnie można wyznaczyć prostą AB = a CD = b 4(CB² − h²) = = (a−b)² 2√CB²−h² = a−b b = a − 2√CB²−h²

	a+b
P +		jak chcesz to moge pomóc bo mi się nudzi
	2

Godzio:

	a+b
P =		* h
	2

edi: Ah, a ja głupi myślałem, że wyznaczenie punktu D jest jednym z poleceń zadania...

Godzio: A zrobiłem bo nie ma nic ciekawego do roboty A(1,1) B(5,5) 5=5a+b 1 =a +b − −−−−−−−−−−−−− 4 = 4a a = 1 y = x

	1+5		1+5
S = [		,		] = [3,3]
	2		2

prosta prostopadła = > a = −1 y = ax + b 3 = −3 +b b = 6 y = −x + 6 => oś symetrii B(5,5) C(3,5) CB = √(5−3)² + (5−5)² = 2 prosta prostopadła do AB i przechodząca przez C : 5 = −3 + b b = 8 y = −x + 8 punkt wspólny tej prostej i AB y₁ = y₂ −x + 8 = x 2x = 8 x = 4 y = 4 E(4,4) wysokość h = EC = √(3−4)² + (5−4)² = √2 a = AB = √32 = 4√2 i tak jak mówiłem wcześniej : b = a − 2√CB²−h² b = 4√2 − 2√4−2 = 4√2 − 2√2 = 2√2

	a+b		6√2
P =		* h =		* √2 = 6
	2		2

tomcio: Bardzo dziękuję za obszerne wyjaśnienie.