Wektory Dream: Punkty P,Q,R są odpowiednio środkami bokow AB,BC,CD rownolegloboku ABCD. Wyznacz współrzędne wierzcholkow rownolegloboku jeżeli P(4,−2) Q(11/2,0) R(1,4) proszę o wytłumaczenie

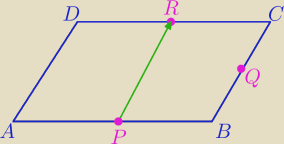
chichi: No wektory, wektory. Rozwiązanie widać gołym okiem, przyda Ci się jeszcze wzór na środek odcinka

Dream: Próbuje i nie wychodzi mi, czy mógłbyś rozwiązać?

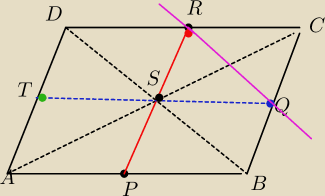
6latek: W srodku S odcinka PR przecinaja sie przekatne rownolegloboku WIec punkt S jest srodkiem jego symetrii Wylicz wspolrzedne S i potem wspolrzedne punktu T ktory jest srodkiem boku AD P=(4,−2) R=(1,4) x_s=2,5 y_s=1

	5
S= (		,1)
	2

Teraz tak patrze na rysunek to wsporzedne T sa niepotrzebne Najwaznieszy jest S Teraz tak 1) Wyznaczasz wspolczynnik kierunkowy prostej PR (nie trzeba pisac calego jej rownania ) 2) Piszesz rownanie prostej rownoleglej do PR i przechodzacej przez Q (czyli prostej przechodzacej przez punkty B i C ) ktore nalezy wyznaczyc Zauwaz ze prosta RQ jest linia srodkowa trojkata DBC wobec tego jest rownolegla do BD (przekatnej rownolegloboku ) 3) Wyznaczasz wspolczynnik kierunkowy prostej RQ 4) Piszesz rownanie prostej rownoleglej do RQ i przechodzacej przez punkt S Dostaniesz rownanie przekatnej BD 5) wyznaczasz wspolrzedne punktu B (przyrownujesz do siebie rownania prostych BD i BC Teraz to juz tylko zabawa ze wzorami na srodek odcinka Masz wspolrzedne punktu B i wspolrzedne punktu Q wynaczasz z ewzoru na srodek odcinka wspolrzedne punktu C Masz wspolrzene punktu B i S wyznaczasz punkt D Masz wspolrzedne punktu C i S wyznaczasz punkt A Nalezy wiedziec ze przekatne rownolegloboku sie polowia A w zadaniu jest jeszcze lepiej bo masz podane srodki Nie jest to wektorami .na razie czytam o wektorach .

chichi:

	3		xB+xC		yB+yC
PQ→=[		,2], R=(		,		)=(1,4) ⇒ xB=2−xC ∧ yB=9−yC
	2		2		2

	3		7		1
BC→=[2xc−2, 2yC−8]=PQ→=[		,2] ⇒ (xC=		∧ yC=5) ⇒ (xB=		∧ yB=3)
	2		4		4

	xA+14		yA+3		31
(		=4 ∧		=−2) ⇒ (xA=		∧ yA=−7)
	2		2		4

	xD+74		11		yD+5		37
(		=		∧		=0) ⇒ (xD=		∧ yD=−5)
	2		2		2		4

	31		1		7		37
A=(		, −7) B=(		, 3) C=(		, 5) D=(		, −5)
	4		4		4		4

Szczęśliwego nowego!

6latek: O i leci na pulpit Jeszcze raz wzajemnie Nie przejmuj sie zakazami . Skoro dla telewizji zniesli zakaz to pewnie beda bac sie krytyki jesli zastosuja to wobec nas

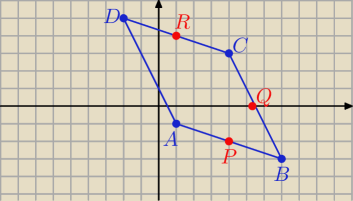
a@b: A(1,−1) , B(7,−3) , C(4,3) , D(−2,5) ========================== → PR=[−3,6] QC=0,5PR[−³₂,3] = [x−¹¹₂,y] ⇒ x_c=4, y_C=3 C(4,3) x_B= 2x_Q−x_C i y_B=2y_Q−y_C ⇒ ............ B(7,−3) x_A=2x_P−x_B i y_A=2y_P−y_B ⇒ ..... A(1,−1) → AD=[−3,6]= [x−x_A, y−y_A] ⇒ x_D=−2 i y_D=5 D(−2,5)

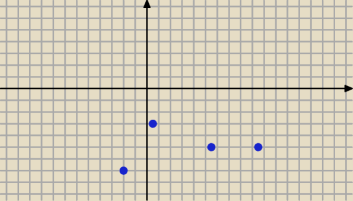
a@b: W/g obliczeń chichi ( na rys. nie ma równoległoboku

a@b: W/g wskazówki 6latka .... to cała "litania"

chichi: Wg rysunku @Eta na temat mojego rozwiązania wszystkie punkty leżą pod osią OX podczas, gdy w moim rozwiązaniu dwa punkty mają dodatnią drugą współrzędną, wasssup?

Filip: Moze a@b juz po trunku

chichi: Ja już jestem po trunku... coś te wierzchołki u mnie też po harnasiu jakimś i wszystko się powirowało haha, ale bez wątpienia wyszedł mi równoległobok To znak, że trzeba odejść już od dziś ode matematyki Zostawiam wam tylko rysunek, na którym moje rozwiązanie to czworokąt ABCD, a @Eta − czworokąt A'B'C'D'

chichi: https://zapodaj.net/66e28ec9ff9b9.png.html

a@b: